Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



2x - xy = 3
x( 2 - y ) = 3
=> TH1 : x = 1
2 - y = 3 => y = -1
TH2 : x = 3
2 - y = 1 => y =1
TH3 : x = -1
2 - y = -3 => y = 5
TH4 : x = -3
2 - y = -1 => y = 3
Vậy các giá trị x;y cần tìm là {(1;-1) ; (3;1) ; (-1;5) ; (-3;3)}
\(x\)(2 - y) = 3
\(x\) = \(\dfrac{3}{2-y}\) (đk y ≠ 0)
\(x\) \(\in\) Z; ⇔ 2 - y \(\in\) Ư(3) = {-3; -1; 1; 3}
Lập bảng ta có:
| 2 - y | -3 | -1 | 1 | 3 |
| y | 5 | 3 | 1 | -1 |
| x = \(\dfrac{3}{2-y}\) | -1 | -3 | 3 | 1 |
Theo bảng trên ta có các cặp \(x;y\) nguyên thỏa mãn đề bài là:
(\(x;y\)) = ( -1; 5); ( -3; 3); (3; 1); (1; -1)

Ta có : AM = \(\dfrac{a}{2}\)
Mà AB = a ( gt )
=> AM = \(\dfrac{AB}{2}\) => AB = 2AM hay M là trung điểm của đoạn thẳng AB
Vậy M là trung điểm của AB

\(\left(\dfrac{6}{5}+\dfrac{5}{6}\right)\times6=\left(\dfrac{36}{30}+\dfrac{25}{30}\right)\times6=\dfrac{61}{30}\times6=\dfrac{366}{30}=122.\)
(6/5+5/6)*6
ta có: quy đồng 2 phân số 6/5 và 5/6 thành 36/30 và 25/30 vậy(36/30+25/30)* 6=61*6=366/30


Giải:
a; Trong một giờ vòi một chảy một mình được: 1 : 10 = \(\dfrac{1}{10}\) (bể)
Trong một giờ vòi hai chảy một mình được: 1 : 6 = \(\dfrac{1}{6}\) (bể)
Trong một giờ hai vòi cùng chảy được: \(\dfrac{1}{10}\) + \(\dfrac{1}{6}\) = \(\dfrac{4}{15}\) (bể)
Cả hai vòi cùng chảy thì sẽ đầy bể sau: 1 : \(\dfrac{4}{15}\) 3,75 (giờ)
b; Trong một giờ vòi ba tháo được: 1 : 15 = \(\dfrac{1}{15}\) (bể)
Trong một giờ ba vòi cùng chảy được:
\(\dfrac{1}{10}+\dfrac{1}{6}-\dfrac{1}{15}\) = \(\dfrac{1}{5}\) (bể)
Mở cả ba vòi khi bể cạn thì sẽ đầy bể sau:
1 : \(\dfrac{1}{5}\) = 5 (giờ)
Kết luận:...
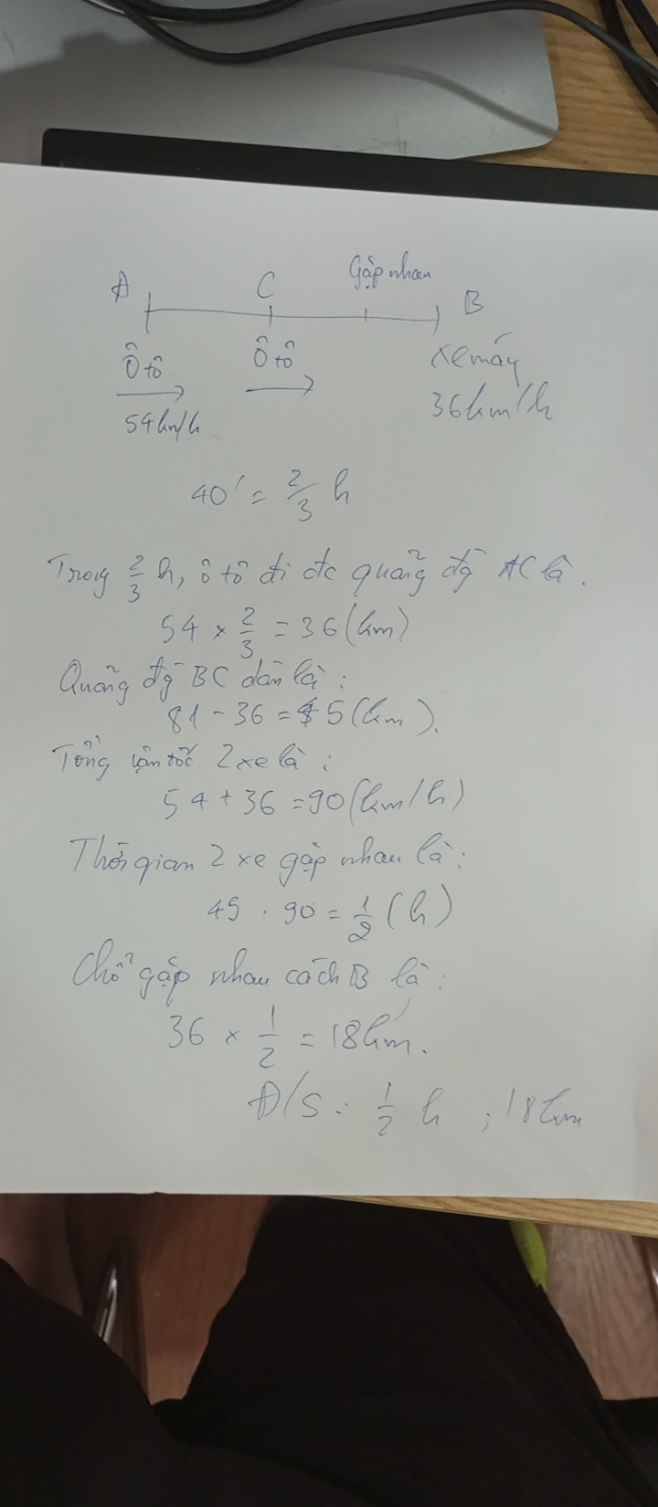













Theo bezout ta có:
F(\(x\)) ⋮ (\(x\) + 1) ⇔ F(-1) = 0
⇒ (-1)2 + 2.(-1) + 3 + a = 0
1 - 2 + 3 + a = 0
2 + a = 0
a = - 2
Vậy với a = - 2 thì \(x^2\) + 2\(x\) + 3 + a ⋮ \(x\) + 1
\(x^2+2x+3+a=\left(x+1\right)^2+2+a\)
Do \(\left(x+1\right)^2\) chia hết \(x+1\) nên đa thức đã cho chia hết \(x+1\) khi \(2+a\) chia hết \(x+1\) với mọi x
\(\Rightarrow2+a=0\)
\(\Rightarrow a=-2\)