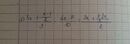Gọi vận tốc đi v₁ (km/h) ; vận tốc về v₂ (km/h) ; thời gian đi là t₁ (h), thời gian về là t₂ (h) ; Quãng đường AB là S (km)

Đổi 30 phút = 1/2 giờ 

Ta có : t₁ = 4 (h)

=> t₂ = 4 - 1/2 = 3,5 (h)

Lại có v₂ - v₁ = 5

=> \(\frac{S}{t_2}-\frac{S}{t_1}=5\)

=> \(S\left(\frac{1}{t^2}-\frac{1}{t^1}\right)=5\)

=> \(S\left(\frac{1}{3.5}-\frac{1}{4}\right)=5\)

=> \(S.\frac{0,5}{14}=5\)

=> S = 140 (km)

Vậy quãng đường AB dài 140 km

giúp mình vs, mình đang cần gấp ạ !!!

\(\frac{1}{x}+2=\left(\frac{1}{x}+2\right)x^2+2ĐK:x\ne0\)

\(\Leftrightarrow\frac{1}{x}+2=\frac{x^2}{x}+2x^2+2\)

\(\Leftrightarrow\frac{1}{x}+2=x+2x^2+2\)

\(\Leftrightarrow\frac{1}{x}-x-2x^2=0\)

\(\Leftrightarrow\frac{1}{x}-\frac{x^2}{x}-\frac{2x^3}{x}=0\Leftrightarrow1-x^2-2x^3=0\)

\(\frac{1}{x}+2=\left(\frac{1}{x}+2\right).x^2+2\left(ĐKXĐ:x\ne0\right)\)

\(\Leftrightarrow\frac{1}{x}+\frac{2x}{x}=\frac{x^2}{x}+\frac{2x^3}{x}+\frac{2x}{x}\)

\(\Rightarrow1+2x=x^2+2x^3+2x\)

\(\Leftrightarrow1+2x-x^2-2x^3-2x=0\)

\(\Leftrightarrow-2x^3-x^2+1=0\)

\(\Leftrightarrow-2x^3+2x-x+1=0\)

\(\Leftrightarrow-2x.\left(x^2-1\right)-\left(x-1\right)=0\)

\(\Leftrightarrow-2x.\left(x-1\right).\left(x+1\right)-\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right).\left[-2x.\left(x+1\right)-1\right]=0\)

\(\Leftrightarrow\left(x-1\right).\left(-2x^2-2x-1\right)=0\)

\(\Leftrightarrow x=1\)(vì \(-2x^2-2x-1\)vô nghiệm)

Vậy phương trình có tập nghiệm là \(S=\left\{1\right\}\)

ĐKXĐ \(x\ne0\)

\(x+\frac{1}{x}=x^2+\frac{1}{x^2}\)

=> \(x^2-x=\frac{1}{x}-\frac{1}{x^2}\)

=> \(\frac{x^2-x}{1}=\frac{x^2-x}{x^3}\)

TH1 : x² -  x = 0

=> x(x - 1) = 0

=> \(\orbr{\begin{cases}x=0\left(\text{loại}\right)\\x=1\end{cases}}\Rightarrow x=1\)

TH2 : x² - x \(\ne0\)

=> x³ = 1 

=> x = 1

Vậy x = 1 là nghiệm của phương trình