Kẻ AH\(\perp\)DC; CK\(\perp\)AB

Ta có: AH\(\perp\)DC

AB//CD
Do đó: AH\(\perp\)AB

mà CK\(\perp\)AB

nên AH//CK

Xét tứ giác AHCK có

AH//CK

AK//CH

Do đó: AHCK là hình bình hành

=>AH=CK

ΔADC có AH là đường cao nên \(S_{ADC}=\dfrac{1}{2}\cdot AH\cdot DC\)

ΔABC có CK là đường cao nên \(S_{ABC}=\dfrac{1}{2}\cdot CK\cdot AB\)

Do đó: \(\dfrac{S_{ABC}}{S_{ADC}}=\dfrac{AB}{CD}=\dfrac{2}{5}\)

=>\(S_{ADC}=\dfrac{5}{2}\cdot S_{ABC}=135\left(cm^2\right)\)

Chu vi đáy là:(6,8+2,8)x2=19,2(cm)

Diện tích xung quanh là:       
             19,2x3=57,6(cm2)

Diện tích 2 đáy là:              6,8x2,8x2=38,08(cm2)

Diện tích toàn phần là:

57,6+38,08=95,68( cm2)

Thể tích là: 6,8x2,8x3=57,12(cm3)

               Đ/s:...... 

đây nha. Tick cho mik nhé 

Chu vi đáy là: (12+8)x2=40(m)

Diện tích xung quanh là:

             40x3,5=140(m2)

Diện tích trần nhà là:

             12x8=96(m2)

Diện tích cần quét sơn là:

            140+96-40=196(m2)

                    Đáp số:196m2.

Bài đây ạ. Tick mik nhé

196m2

a.

Thời gian anh Hà đi từ tỉnh A đến tỉnh B là:

\(150:50=3\) (giờ)

Anh Hà đến tỉnh B lúc:

7 giờ 15 phút + 3 giờ = 10 giờ 15 phút

b.

Đổi 2 giờ 20 phút =7/3 giờ

Sau 2 giờ 20 phút anh Hà đi được quãng đường là:

\(45\times\dfrac{7}{3}=105\left(km\right)\)

Anh Hà còn cách tỉnh A số kilomet là:

\(150-105=45\left(km\right)\)

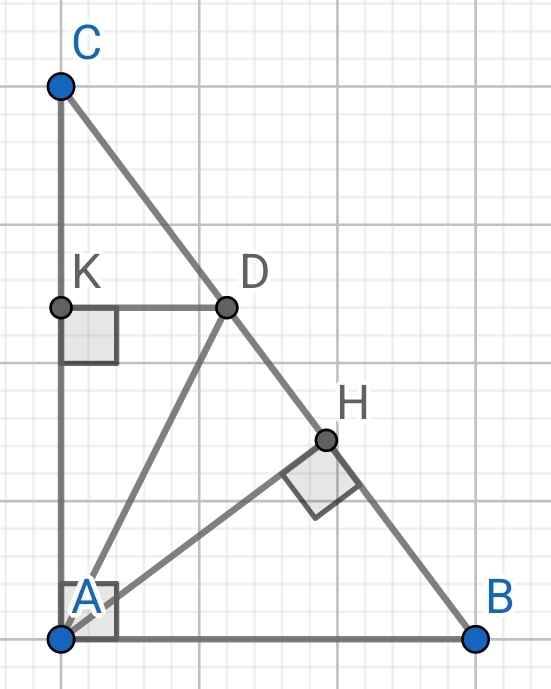
a) ∆ABD có:

BA = BD (gt)

⇒ ∆ABD cân tại B

⇒ ∠BAD = ∠BDA

b) Do DK ⊥ AC (gt)

AB ⊥ AC (do ∆ABC vuông tại A)

⇒ DK // AB

⇒ ∠ADK = ∠BAD (so le trong)

Mà ∠BAD = ∠BDA (cmt)

⇒ ∠ADK = ∠BDA

⇒ ∠ADK = ∠HDA

Xét hai tam giác vuông: ∆ADK và ∆ADH có:

AD là cạnh chung

∠ADK = ∠HDA (cmt)

⇒ ∆ADK = ∆ADH (cạnh huyền - góc nhọn)

⇒ ∠DAK = ∠DAH (hai góc tương ứng)

⇒ ∠DAC = ∠DAH

⇒ AD là tia phân giác của ∠HAC

c) Do ∆ADK = ∆ADH (cmt)

⇒ AK = AH (hai cạnh tương ứng)

d) ∆CDK vuông tại K

⇒ CD là cạnh huyền nên là cạnh lớn nhất

⇒ CK < CD

Mà AK = AH (cmt)

BA = BD (cmt)

Cộng vế với vế, ta có:

CK + AK + AB < CD + AH + BD

⇒ AB + AC < BC + AH

a: Xet ΔBAD có BA=BD

nên ΔBAD cân tại B

=>\(\widehat{BAD}=\widehat{BDA}\)

b: Ta có: \(\widehat{HAD}+\widehat{BDA}=90^0\)(ΔDHA vuông tại H)

\(\widehat{DAC}+\widehat{BAD}=90^0\)

mà \(\widehat{BDA}=\widehat{BAD}\)

nên \(\widehat{HAD}=\widehat{DAC}\)

=>AD là phân giác của góc HAC

c: Xét ΔAHD vuông tại H và ΔAKD vuông tại K có

AD chung

\(\widehat{HAD}=\widehat{KAD}\)

Do đó: ΔAHD=ΔAKD

=>AH=AK

d: Xét ΔABC có AH là đường cao

nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot AB\cdot AC\)

=>\(AH\cdot BC=AB\cdot AC\)

\(\left(AB+AC\right)^2-\left(BC+AH\right)^2\)

\(=AB^2+AC^2+2\cdot AB\cdot AC-BC^2-AH^2-2\cdot BC\cdot AH\)

\(=BC^2+2\cdot AH\cdot BC-BC^2-2\cdot BC\cdot AH-AH^2\)

\(=-AH^2< 0\)

=>\(\left(AB+AC\right)^2< \left(BC+AH\right)^2\)

=>AB+AC<BC+AH

Bài 8: y=(a+1)x+5

a: Thay x=5 và y=2 vào y=(a+1)x+5, ta được:

5(a+1)+5=2

=>5(a+1)=-3

=>\(a+1=-\dfrac{3}{5}\)

=>\(a=-\dfrac{3}{5}-1=-\dfrac{8}{5}\)

b: Thay x=3 và y=6 vào y=(a+1)x+5, ta được:

\(3\left(a+1\right)+5=6\)

=>3a+8=6

=>3a=-2

=>\(a=-\dfrac{2}{3}\)

25kg

25 kg bạn ạ 

\(\dfrac{240}{1}-\dfrac{9}{15}=240-0,6=239,4\)

4503x8+3497x8

=8(4503+3497)

=8000x8

=64000

=8x(4503+3497)

=8x8000

=64000

Giả sử mỗi con thỏ có 2 chân

Do số gà nhiều hơn số thỏ là 30 con nên nhiều hơn số chân là:

30 × 2 = 60 (chân)

Thực tế mỗi con thỏ nhiều hơn mỗi con gà số chân là:

4 - 2 = 2 (chân)

Số con thỏ là:

(60 - 24) : 2 = 18 (con)

Số con gà là:

18 + 30 = 48 (con)