 gấpppp giúppp e vsss
gấpppp giúppp e vsss
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AO là đường trung trực của BC
b: Xét (O) có
ΔCBD nội tiếp
CD là đường kính
Do đó: ΔCBD vuông tại B
=>CB\(\perp\)BD
mà AO\(\perp\)BC
nên AO//BD

Tuổi hiện nay của ông là:
(78+60):2=138:2=69(tuổi)
Tuổi cháu hiện nay là 69-60=9(tuổi)

a: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(30^0< 100^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
=>\(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
=>\(\widehat{yOz}=100^0-30^0=70^0\)
Vì tia Ot nằm trong góc yOz
nên tia Ot nằm giữa hai tia Oy,Oz
=>\(\widehat{yOt}+\widehat{zOt}=\widehat{yOz}\)
=>\(\widehat{zOt}=70^0-20^0=50^0\)
Vì \(\widehat{yOt}< \widehat{zOt}\left(20^0< 50^0\right)\)
nên Ot không là phân giác của góc yOz
b: Vì \(\widehat{zOt}< \widehat{zOx}\left(50^0< 100^0\right)\)
nên tia Ot nằm giữa hai tia Oz và Ox
=>\(\widehat{tOz}+\widehat{tOx}=\widehat{xOz}\)
=>\(\widehat{xOt}=100^0-50^0=50^0\)
Ta có: tia Ot nằm giữa hai tia Ox và Oz
mà \(\widehat{xOt}=\widehat{zOt}\left(=50^0\right)\)
nên Ot là phân giác của góc xOz

\(2\cdot4\cdot8\cdot8\cdot8\cdot8\cdot2\cdot2\cdot2=2\cdot2^2\cdot2^3\cdot2^3\cdot2^3\cdot2^3\cdot2\cdot2\cdot2=2^{1+2+3+3+3+3+1+1+1}=2^{18}\)

a: Gọi số cần tìm là x
Vi x chia hết cho cả 8;12;16 nên \(x\in BC\left(8;12;16\right)\)
=>\(x\in B\left(48\right)\)
=>\(x\in\left\{48;96;144;192;...\right\}\)
mà 100<x<140
nên \(x\in\varnothing\)
b: Gọi số cần tìm là x
\(12=2^2\cdot3;18=2\cdot3^2;21=3\cdot7\)
=>\(BCNN\left(12;18;21\right)=2^2\cdot3^2\cdot7=252\)
Vì x chia 12;18;21 đều dư 5 nên \(x-5\in BC\left(12;18;21\right)\)
=>\(x-5\in B\left(252\right)\)
=>\(x-5\in\left\{0;252;504;756;1008;...\right\}\)
=>\(x\in\left\{5;257;509;761;1013;...\right\}\)
mà số đó xấp xỉ 1000
nên x=1013
c: Gọi số học sinh khối 6 là x(bạn)
(Điều kiện: \(x\in Z^+\))
Vì số học sinh khi xếp hàng 11 thì không dư nên \(x\in B\left(11\right)\)(2)
Vì số học sinh xếp hàng 10;12;15 đều dư 3 bạn nên \(x-3\in BC\left(10;12;15\right)\)
=>\(x-3\in B\left(60\right)\)
=>\(x-3\in\left\{60;120;180;240;300;360;420;...\right\}\)
=>\(x\in\left\{63;123;183;243;303;363;423;...\right\}\)
mà 0<x<400
nên \(x\in\left\{63;123;183;243;303;363\right\}\left(1\right)\)
Từ (1),(2) suy ra x=363(nhận)
Vậy: Số học sinh khối 6 là 363 bạn
a) Gọi số cần tìm là: a (a ϵ N*; 100 < a < 140)
Ta có:
8 = 23
12 = 22.3
16 = 24
BCNN (8; 12; 16) = 24.3 = 48
a ϵ BC(8; 12; 16) ϵ B(48) ϵ {0; 48; 96; 144; ...}
⇒ Không có số tự nhiên thoả mãn đề bài
b) Gọi số cần tìm là a (a ϵ N; a \(\approx\) 1000)
Do chia cho 12; 18; 21 đều dư 5
⇒ (a - 5) ⋮ 12
⇒ (a - 5) ⋮ 18
⇒ (a - 5) ⋮ 21
Ta có:
12 = 22.3
18 = 2.32
21 = 3.7
BCNN(12; 18; 21) = 22.32.7 = 252
a ϵ BC(12; 18; 21) ϵ B(252) ϵ {0;252; 504; 756; 1008; ...}
Trong các số trong tập hợp B(252); 1008 là số gần với 1000 nhất
⇒ a = 1008 + 5 = 1023
c) Gọi số cần tìm là a (a ϵ N; a< 400}
Ta có:
(a - 3) ⋮ 10
(a - 3) ⋮ 12
(a - 3) ⋮ 15
a ⋮ 11
Ta có:
10 = 2.5
12 = 22.3
15 = 3.5
BCNN(10; 12; 15) = 22.3.5 = 60
(a - 3) ϵ B(60) ϵ {0; 60; 120; 180; 240; 300; 360; 420; ...}
⇒ a ϵ {3; 63; 123; 183; 243; 303; 363; 423; ...}
Do 363 < 40 và ⋮ cho 11 nên a = 363

\(\left(1+\dfrac{1}{100}\right)\times\left(1+\dfrac{1}{101}\right)\times\left(1+\dfrac{1}{102}\right)\times...\times\left(1+\dfrac{1}{2012}\right)\)
\(=\dfrac{101}{100}\times\dfrac{102}{101}\times\dfrac{103}{102}\times...\times\dfrac{2013}{2012}\)
\(=\dfrac{101\times102\times103\times...\times2013}{100\times101\times102\times...\times2012}\)
\(=\dfrac{2013}{100}\)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}=\dfrac{3}{4}\)
nên \(\widehat{C}\simeq37^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-37^0=53^0\)
b: Xét ΔBDC vuông tại B có BA là đường cao
nên \(BA^2=AD\cdot AC\)
=>\(AD=\dfrac{3^2}{4}=\dfrac{9}{4}=2,25\left(cm\right)\)
ΔABD vuông tại A
=>\(AB^2+AD^2=BD^2\)
=>\(BD=\sqrt{2,25^2+3^2}=3,75\left(cm\right)\)
Xét ΔBAD vuông tại A có AF là đường cao
nên \(BF\cdot BD=BA^2\left(1\right)\)
Xét ΔBAC vuông tại A có AE là đường cao
nên \(BE\cdot BC=BA^2\left(2\right)\)
Từ (1),(2) suy ra \(BF\cdot BD=BE\cdot BC\)
Xét tứ giác AEBF có \(\widehat{AEB}=\widehat{AFB}=\widehat{EBF}=90^0\)
nên AEBF là hình chữ nhật
ΔABC vuông tại A có AE là đường cao
nên \(\left\{{}\begin{matrix}AE\cdot BC=AB\cdot AC\\BE\cdot BC=BA^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AE=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\\BE=\dfrac{3^2}{5}=1,8\left(cm\right)\end{matrix}\right.\)
AEBF là hình chữ nhật
=>\(S_{AEBF}=AE\cdot BE=2,4\cdot1,8=4,32\left(cm^2\right)\)
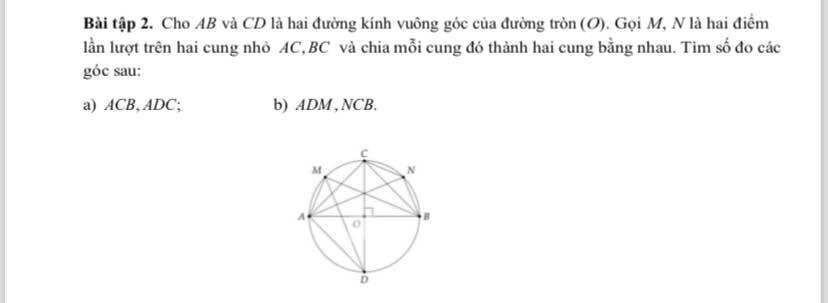
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>\(\widehat{ACB}=90^0\)
Xét (O) có \(\widehat{ADC}\) là góc nội tiếp chắn cung AC
nên \(\widehat{ADC}=\dfrac{\widehat{AOC}}{2}=\dfrac{90^0}{2}=45^0\)
b: M là điểm chia cung AC thành hai cung nhỏ bằng nhau
=>\(sđ\stackrel\frown{MA}=\dfrac{sđ\stackrel\frown{AC}}{2}=\dfrac{90^0}{2}=45^0\)
Xét (O) có \(\widehat{ADM}\) là góc nội tiếp chắn cung AM
nên \(\widehat{ADM}=\dfrac{1}{2}\cdot sđ\stackrel\frown{MA}=\dfrac{1}{2}\cdot45^0=22,5^0\)
N chia cung BC thành hai cung nhỏ bằng nhau
=>\(sđ\stackrel\frown{BN}=\dfrac{sđ\stackrel\frown{BC}}{2}=45^0\)
Xét (O) có
\(\widehat{NCB}\) là góc nội tiếp chắn cung NB
=>\(\widehat{NCB}=\dfrac{sđ\stackrel\frown{NB}}{2}=\dfrac{45^0}{2}=22,5^0\)