Giờ thứ hai cho rồi mà em, em xem lại đề nhé.

Các số tự nhiên thỏa mãn đề bài:

\(489;579;678\)

Vậy có 3 số thỏa mãn

Vì c là số lẻ, ta có thể biểu diễn nó dưới dạng c = 2k + 1, với k là một số nguyên dương.

Substitute giá trị của c vào phương trình a + b + c = 21 ta có:

a + b + 2k + 1 = 21

a + b = 20 - 2k

Vì a < b < 21 - a - b, ta có thể thay bằng biến x và sử dụng phương pháp bisection để tìm nghiệm của x bằng cách tìm giá trị k thích hợp. Đặt f(k) = a + x + 2k + 1 - 21.

Vì a và x là số lẻ nên a + x là số chẵn, khi đó f(k) cũng là số chẵn.

Ta có thể kiểm tra giá trị của f(k) để tìm giá trị của x. Lưu ý rằng k phải thỏa mãn điều kiện k ≤ (21 - 1)/2 = 10.

Như vậy, để tìm số lẻ có ba chữ số thoả mãn điều kiện a < b < c và a + b + c = 21, ta có thể thực hiện các bước sau:

• Thử từng giá trị của k từ 1 đến 10:

• Với mỗi k, tính giá trị của f(k) = a + x + 2k + 1 - 21
• Nếu f(k) = 0 và a, x là số lẻ thì đó là một bộ số thỏa mãn. Nếu f(k) ≠ 0 hoặc a, x không phải số lẻ thì tiếp tục thử k tiếp theo.

• Tổng hợp tất cả các bộ số thỏa mãn để có số lẻ có ba chữ số thoả mãn yêu cầu của bài toán.

Ví dụ, thử với k = 1, ta có:

a + x = 20 - 2(1) = 18

f(1) = a + x + 3 - 21 = a + x - 18

Nếu a + x là số lẻ, thì ta phải có a + x - 18 là số lẻ và bằng 1, 3, 5, 7 hoặc 9.

• Nếu a + x - 18 = 1, ta có a + x = 19, vậy có một bộ số là (9,9,3).
• Nếu a + x - 18 = 3, ta có a + x = 21, vậy không có bộ số nào là số lẻ và thoả mãn điều kiện.
• Nếu a + x - 18 = 5, ta có a + x = 23, vậy không có bộ số nào là số lẻ và thoả mãn điều kiện.
• Nếu a + x - 18 = 7, ta có a + x = 25, vậy có một bộ số là (7,11,3).
• Nếu a + x - 18 = 9, ta có a + x = 27, vậy không có bộ số nào là số lẻ và thoả mãn điều kiện.

Vậy có hai số lẻ có ba chữ số thoả mãn yêu cầu của bài toán, đó là 793 và 911.

Đề sai, em ghi đề cho chính xác lại

\(\dfrac{178\times270+156}{179\times270-114}\)

\(=\dfrac{270\left(156+22\right)+156}{270\left(156+23\right)-114}\)

\(=\dfrac{270\times156+6096}{270\times156+6096}=1\)

chiều dài hơn chiều rộng bao nhiêu m vậy em?

Hơn1 ạ

Câu 3:

a: 

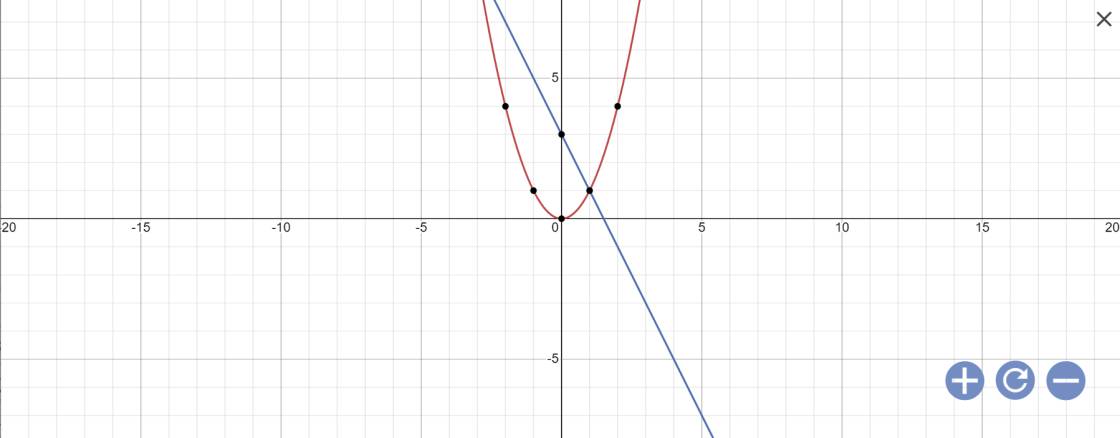
b: Phương trình hoành độ giao điểm là:

\(x^2=-2x+3\)

=>\(x^2+2x-3=0\)

=>(x+3)(x-1)=0

=>\(\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)

Khi x=-3 thì \(y=\left(-3\right)^2=9\)

Khi x=1 thì \(y=1^2=1\)

Vậy: (P) cắt (d) tại A(-3;9); B(1;1)

Câu 4:

a:

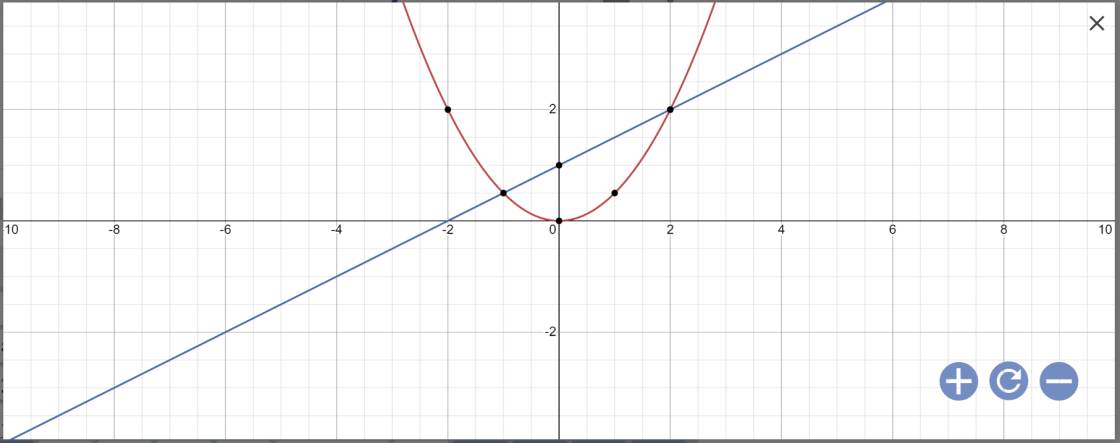
b: Phương trình hoành độ giao điểm là:

\(\dfrac{1}{2}x^2=\dfrac{1}{2}x+1\)

=>\(x^2=x+2\)

=>\(x^2-x-2=0\)

=>(x-2)(x+1)=0

=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)

Khi x=2 thì \(y=\dfrac{1}{2}\cdot2^2=2\)

Khi x=-1 thì \(y=\dfrac{1}{2}\cdot\left(-1\right)+1=1-\dfrac{1}{2}=\dfrac{1}{2}\)

vậy: \(A\left(2;2\right);B\left(-1;\dfrac{1}{2}\right)\)

c: Thay x=1 vào (P), ta được:

\(y=\dfrac{1}{2}\cdot1^2=\dfrac{1}{2}\)

vậy: C(1;0,5)

A(2;2); B(-1;0,5); C(1;0,5)

\(AB=\sqrt{\left(-1-2\right)^2+\left(0,5-2\right)^2}=\dfrac{3\sqrt{5}}{2}\)

\(AC=\sqrt{\left(1-2\right)^2+\left(0,5-2\right)^2}=\dfrac{\sqrt{13}}{2}\)

\(BC=\sqrt{\left(1+1\right)^2+\left(0,5-0,5\right)^2}=2\)

Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{\dfrac{45}{4}+\dfrac{13}{4}-4}{2\cdot\dfrac{3\sqrt{5}}{2}\cdot\dfrac{\sqrt{13}}{2}}=\dfrac{7}{\sqrt{65}}\)

=>\(sinBAC=\sqrt{1-\left(\dfrac{7}{\sqrt{65}}\right)^2}=\dfrac{4}{\sqrt{65}}\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)

\(=\dfrac{1}{2}\cdot\dfrac{4}{\sqrt{65}}\cdot\dfrac{3\sqrt{5}}{2}\cdot\dfrac{\sqrt{13}}{2}=\dfrac{3}{2}\)

  Giải

Số cần tìm là:

(80% : 2 - 0,075) x 6 = 1,95

Số cần tìm là 1,95 

Câu 2: \(\dfrac{x}{6}+\dfrac{y}{8}=1\)

=>\(\dfrac{4x+3y}{24}=1\)

=>4x+3y=24

=>4x+3y-24=0

Khoảng cách từ O đến đường thẳng 4x+3y-24=0 là:

\(d\left(O;4x+3y-24=0\right)=\dfrac{\left|0\cdot4+0\cdot3-24\right|}{\sqrt{3^2+4^2}}=\dfrac{24}{5}=4,8\)