Tìm phân số bằng phân số\(\dfrac{-33}{57}\) biết rằng tổng của tử và mẫu của phân số bằng 24
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


cả diện tích xung quanh và diện tích toàn phần tăng lên 4 lần nhé
cho mình xu nhé

\(\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+...+\dfrac{1}{n.\left(n+1\right)}=\dfrac{3}{10}\)
\(\Rightarrow\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{3}{10}\)
\(\Rightarrow\dfrac{1}{3}-\dfrac{1}{n+1}=\dfrac{3}{10}\)
\(\Rightarrow\dfrac{1}{n+1}=\dfrac{1}{30}\)
\(\Rightarrow n+1=30\)
\(\Rightarrow n=29\)
Vậy n = 29.

Ta có: \(\dfrac{-371}{-459}=\dfrac{371}{459}\) là một số dương
=> \(\dfrac{-371}{-459}>\dfrac{-371}{159}\)


\(-\dfrac{5}{8}-x=\dfrac{1}{6}-2x\)
\(\Rightarrow-\dfrac{5}{8}-x-\dfrac{1}{6}+2x=0\)
\(\Rightarrow-\dfrac{19}{24}+x=0\)
\(\Rightarrow x=\dfrac{19}{24}\)
Vậy \(x=\dfrac{19}{24}\).

gọi số tự nhiên đó là a ( a thuộc z)
do a chia 3 dư 2; chia 5 dư 3 => a+1 chia hết cho 3 và 5
=> a+1 thuộc bc của 3 và 5
3=3 ; 5=5 => bcnn của 3 và 5 = 3.5=15
bc của 3 và 5 thuộc {0;15;30;.....}
=> a+1 thuộc {0;15;30;...}
=> a thuộc { 14; 29;......} ( vì a thuộc N)
Mà a nhỏ nhất a chia 7 dư 2 nên a = 44
Vậy
Ta có thể giải bài toán này bằng cách sử dụng định lý dư dấu của Trung tâm Đa dạng (Chinese Remainder Theorem).
Gọi số tự nhiên cần tìm là x. Theo yêu cầu đề bài, ta có hệ phương trình tương đương sau:
x ≡ 2 (mod 3) x ≡ 3 (mod 5) x ≡ 2 (mod 7)
Theo định lý dư dấu, hệ phương trình này có nghiệm duy nhất modulo 3x5x7 = 105.
Để tìm nghiệm của hệ phương trình, ta có thể áp dụng thuật toán quy hoạch động (Dynamic Programming) như sau:
- Đặt i = 2, và x = 2. Ta kiểm tra xem x có thỏa mãn điều kiện thứ hai (x ≡ 3 (mod 5)) không. Nếu không, ta tăng giá trị x lên 105 (vì 105 chia hết cho cả 3, 5 và 7), và quay lại bước kiểm tra. Nếu x thỏa mãn điều kiện thứ hai, ta tiếp tục đến bước tiếp theo.
- Đặt i = 3, và x = 2. Ta kiểm tra xem x có thỏa mãn điều kiện thứ ba (x ≡ 2 (mod 7)) không. Nếu không, ta tăng giá trị x lên 105, và quay lại bước kiểm tra. Nếu x thỏa mãn điều kiện thứ ba, ta đã tìm được nghiệm của hệ phương trình.
Do đó, số tự nhiên nhỏ nhất cần tìm là 2 + 3x3x7 = 65. Vì vậy, khi chia 3 dư 2, chia 5 dư 3 và chia 7 dư 2, số tự nhiên nhỏ nhất là 65.

)
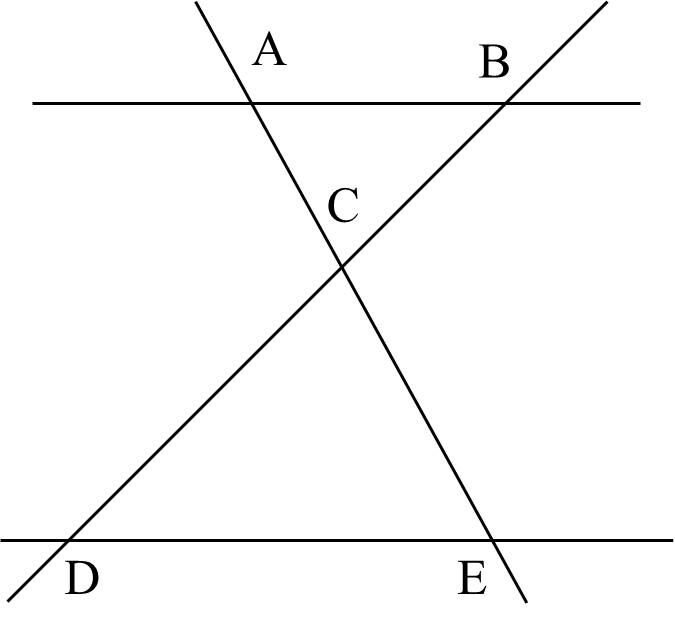
a) Tập hợp các điểm thuộc đoạn thẳng ��BD là �;�;�B;C;D, tập hợp các điểm thuộc không đoạn thẳng ��BD là �;�A;E.
b) Cặp đường thẳng song song là ��AB // ��DE.
c) Gợi ý: Liệt kê theo các giao điểm, có 5 giao điểm nên có 5 cặp đường thẳng cắt nhau.
Các cặp đường thẳng cắt nhau là
��AB và ��AE cắt nhau tại �A.
��BA và ��BD cắt nhau tại �B.
��AE và ��BD cắt nhau tại �C.
��DE và ��DB cắt nhau tại �D.
��EA và ��ED cắt nhau tại �E.
2)
a)
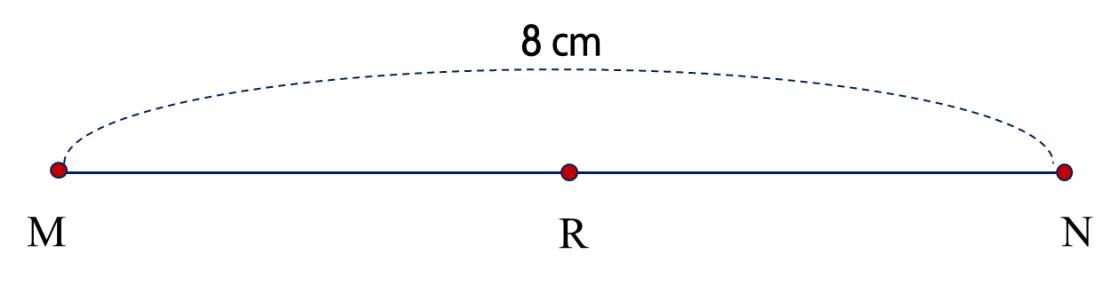
Vì �R là trung điểm của đoạn thẳng ��MN, nên ta có ��=��=��:2MR=RN=MN:2.
Độ dài của đoạn thẳng ��MR hay ��RN là:
8:2=48:2=4 (cm)
b)
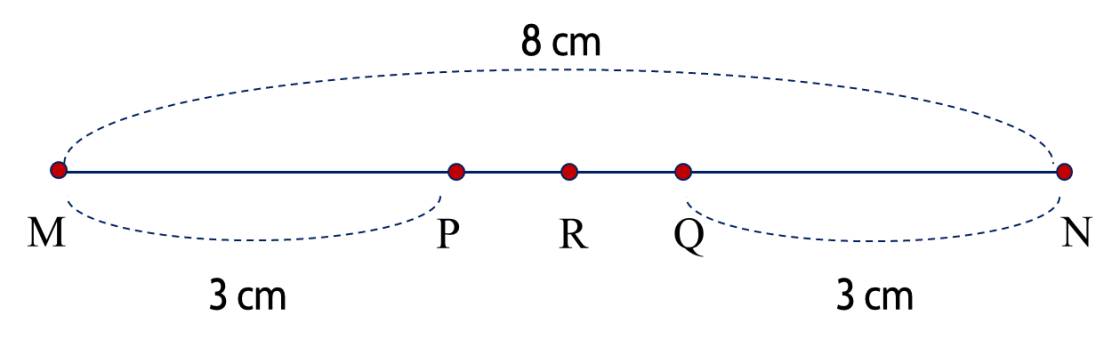
Nhìn hình vẽ, ta thấy �R nằm giữa �P và �Q; ��=��+��+��MN=MP+PQ+QN; ��=��+��MR=MP+PR.
Độ dài của đoạn thẳng ��PQ là
8−3−3=28−3−3=2 (cm).
Độ dài của đoạn thẳng ��PR là
4−3=14−3=1 (cm).
Từ đây, ta thấy ��:��=12PR:PQ=21,
Vậy �R là trung điểm ��PQ.
3)
Chọn 1 điểm nối với 1111 điểm còn lại ta được 1111 đường thẳng, làm như thế với 1212 điểm ta được 12.(12−1)=13212.(12−1)=132 đường thẳng. Nhưng mỗi đường thẳng lặp lại 22 lần nên số đường thẳng vẽ được là 132:2=66132:2=66 đường thẳng.
Qua 44 điểm không thẳng hàng sẽ vẽ được 66 đường thẳng.
Qua 44 điểm thẳng hàng vẽ được 11 đường thẳng nên số đường thẳng giảm đi 55 đường thẳng
Vậy số đường thẳng vẽ được là 66−5=6166−5=61 đường thẳng vậy ta vẽ được 61 đường thẳng.
a, các điểm thuộc đường thẳng BD là: E
b, các cặp đường thẳng song song là; AB với DE
c, AE cắt BD ở giao điểm E
2)
điểm MR = 4cm
điểm RN=4cm
b, R có là trung điểm của PQ, vì ta lấy MR trừ cho MP tương tự với phía bên kia ta lấy RN trừ cho QN ta ra được kết quả bằng 1cm
3

gọi số thứ nhất là x , số thứ hai là 2015 - x
Theo bài ra ta có : x.\(\dfrac{2}{3}\). \(\dfrac{6}{7}\) - (2015 - x). \(\dfrac{4}{5}\). \(\dfrac{5}{6}\) = 52
\(\dfrac{4}{7}\). x - ( 2015 - x) . \(\dfrac{2}{3}\) = 52
12x - 14. 2015 + 14x = 1092
26x = 1092 + 28210
26x = 29302
\ x = 29302 : 26
x = 1127
Số thứ hai là : 2015 - 1127 = 888
kết luận : số thứ nhất 1127; số thứ hai 888
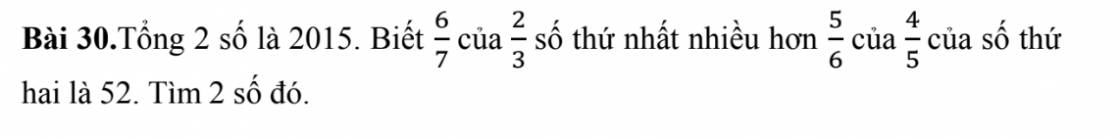
\(\dfrac{-33}{57}=\dfrac{-11}{29}\Rightarrow\)Phân số cần tìm có dạng: \(\dfrac{-11k}{29k}\)
Theo bài ra ta có: -11k + 29k = 24
=> 18k = 24
=> k = \(\dfrac{12}{9}\)
Vậy phân số cần tìm là: \(\dfrac{-11.\dfrac{12}{9}}{29.\dfrac{12}{9}}=\dfrac{-44}{3}:\dfrac{116}{3}=\dfrac{-44}{116}\)