cho tập hợp A={xx en và x <11} chọn điền "e" hoặc "e/" thích hợp vào chỗ chấm 7 A ;11 A;0 A;13 A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{27\cdot45+27\cdot5}{2+4+6+...+14+16+18}\)
\(=\dfrac{27\left(45+5\right)}{\left(2+18\right)+\left(4+16\right)+\left(6+14\right)+\left(8+12\right)+10}\)
\(=\dfrac{27\cdot50}{20+20+20+20+10}=\dfrac{27\cdot50}{90}=27\cdot\dfrac{5}{9}=15\)
\(\dfrac{27\cdot45+27\cdot5}{2+4+6+...+18}\\ =\dfrac{27\cdot\left(45+5\right)}{\dfrac{\left[\left(18-2\right):2+1\right]\left(18+2\right)}{2}}\\ =\dfrac{27\cdot50}{\dfrac{\left(16:2+1\right)\cdot20}{2}}\\ =\dfrac{27\cdot50}{\left(8+1\right)\cdot10}\\ =\dfrac{27\cdot50}{9\cdot10}\\ =15\)

\(A=10^3+\left[20^2+\left(2^3\cdot3\cdot5-3^2\cdot5\right)\right]\\ =10^3+\left[20^2+\left(8\cdot3\cdot5-9\cdot5\right)\right]\\ =10^3+\left[20^2+\left(120-45\right)\right]\\ =1000+\left(400+75\right)\\ =1000+475\\ =1475\)
\(B=326+8\cdot\left[20^2+\left(65-5\cdot11\right)\right]\\ =326+8\cdot\left[20^2+\left(65-55\right)\right]\\ =326+8\cdot\left(400+10\right)\\ =326+8\cdot410\\ =326+3280\\ =3606\)

`#3107.101107`
`99 - 97 + 95 - 93 + ... + 3 - 1`
Số hạng của tổng trên:
`(99 - 1) \div 2 + 1 = 50`
Số cặp có trong tổng trên:
`50 \div 2 = 25` (cặp)
__
`99 - 97 + 95 - 93 + ... + 3 - 1`
`= (99 - 97) + (95 - 93) + ... + (3 - 1)`
`= 2 + 2 + ... + 2`
Tổng trên có `25` cặp `\rightarrow` Có `25` số `2`
`= 2 \times 25 = 50.`

a) Mỗi số lẻ liên tiếp cách nhau 2 đơn vị mà đây là dãy tăng dần nên:
a = 17 + 2 = 19
b = 19 + 2 = 21
b) Mỗi số tự nhiên liên tiếp cách nhau 1 đơn vị mà đây là dãy giảm dần nên:
m = 101 + 1 = 102
n = 101 - 1 = 100
p = 100 - 1 = 99
Ta có:
2020 < 2021
a) Nếu a > 2021 thì a > 2020
b) a < 2020

\(A=\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+...+\dfrac{2023}{2^{2023}}\\ 2A=1+\dfrac{2}{2}+\dfrac{3}{2^2}+...+\dfrac{2023}{2^{2022}}\\ 2A-A=\left(1+\dfrac{2}{2}+\dfrac{3}{2^2}+...+\dfrac{2023}{2^{2022}}\right)-\left(\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+...+\dfrac{2023}{2^{2023}}\right)\\ A=1+\left(\dfrac{2}{2}-\dfrac{1}{2}\right)+\left(\dfrac{3}{2^2}-\dfrac{2}{2^2}\right)+...+\left(\dfrac{2023}{2^{2022}}-\dfrac{2022}{2^{2022}}\right)+\dfrac{2023}{2^{2023}}\\ A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2022}}+\dfrac{2023}{2^{2023}}\\ 2A=2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2021}}+\dfrac{2023}{2^{2023}}\\ 2A-A=\left(3+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}+\dfrac{2023}{2^{2023}}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2022}}\right)\\ A=\left(3-1\right)+\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+\left(\dfrac{1}{2^2}-\dfrac{1}{2^2}\right)+...+\left(\dfrac{1}{2^{2021}}-\dfrac{1}{2^{2021}}\right)-\dfrac{2023}{2^{2023}}-\dfrac{1}{2^{2022}}\\ A=2-\dfrac{2023+2}{2^{2023}}\\ A=2-\dfrac{2025}{2^{2023}}< 2\\ \)
@ Phong Lần sau em nên chú ý về dấu như vậy bài làm sẽ hoàn hảo em nhé!

Gọi ba số tự nhiên liên tiếp là a;a+1;a+2
Tổng của ba số là 264 nên a+a+1+a+2=264
=>3a=261
=>a=261:3=87
Vậy: Ba số tự nhiên liên tiếp cần tìm là 87;87+1=88;87+2=89

Gọi ba số tự nhiên chẵn liên tiếp là a;a+2;a+4
Tổng của số lớn nhất và số bé nhất là 644 nên a+a+4=644
=>2a=640
=>a=320
Vậy: ba số cần tìm là 320;320+2=322;320+4=324

\(A=2023.2023=2023^2\)
\(B=2021.2025=\left(2023-2\right)\left(2023+2\right)=2023^2-4\)
=> A > B
B = 2021 x 2025
B = (2023 - 2) x (2023 + 2)
B = 2023 x 2023 + 2023 x 2 - 2 x 2023 - 4
B = 2023 x 2023 + [2 x (2023 - 2023) - 4]
B = 2023 x 2023 + (2 x 0 - 4)
B = 2023 x 2023 + (0 - 4)
B = 2023 x 2023 - 4
B = A - 4
Vậy A > B và lớn hơn 4 đơn vị.
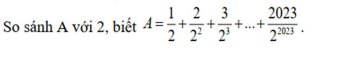
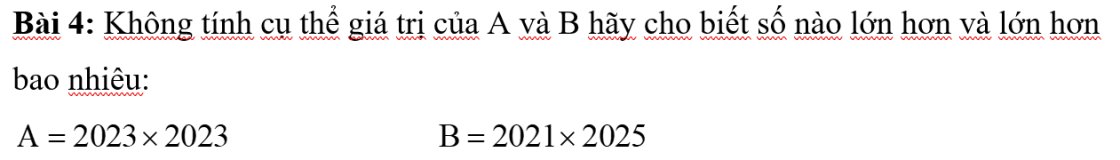
giúp với
\(7\in A;11\notin A;0\in A;13\notin A\)