Vẽ đồ thị hệ số trên cùng 1 Mp toạ độa,y=x-1 và y=-2x-4.
b,tìm toạ độ giao đầu c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne4\end{matrix}\right.\)
\(P=\left(\dfrac{2}{x-4}+\dfrac{1}{\sqrt{x}+2}\right):\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+2}{1}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
Để P=3/2 thì \(\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{3}{2}\)
=>\(3\left(\sqrt{x}-2\right)=2\sqrt{x}\)
=>\(3\sqrt{x}-2\sqrt{x}=6\)
=>\(\sqrt{x}=6\)
=>x=36(nhận)

Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
=>AH=DE
Xét ΔABH vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\)
\(AD\cdot AB+AE\cdot AC=AH^2+AH^2\)
\(=2AH^2=2DE^2\)

\frac{\sqrt{\left(6.2\right)^{2}-\left(5.9\right)^{2}}}{\sqrt{2.43}}

\(A=2\sqrt{2}\left(\dfrac{a}{2\sqrt{2b\left(a+b\right)}}+\dfrac{b}{2\sqrt{2c\left(b+c\right)}}+\dfrac{a}{2\sqrt{2a\left(c+a\right)}}\right)\)
\(A\ge2\sqrt{2}\left(\dfrac{a}{2b+a+b}+\dfrac{b}{2c+b+c}+\dfrac{a}{2a+c+a}\right)\)
\(A\ge2\sqrt{2}\left(\dfrac{a^2}{a^2+3ab}+\dfrac{b^2}{b^2+3bc}+\dfrac{c^2}{c^2+3ca}\right)\)
\(A\ge\dfrac{2\sqrt{2}\left(a+b+c\right)^2}{a^2+b^2+c^2+3\left(ab+bc+ca\right)}=\dfrac{2\sqrt{2}\left(a+b+c\right)^2}{\left(a+b+c\right)^2+ab+bc+ca}\)
\(A\ge\dfrac{2\sqrt{2}\left(a+b+c\right)^2}{\left(a+b+c\right)^2+\dfrac{1}{3}\left(a+b+c\right)^2}=\dfrac{3\sqrt{2}}{2}\)
Dấu "=" xảy ra khi \(a=b=c\)
Bổ sung các bđt được áp dụng trong bài thầy Lâm cho rõ ràng:
Áp dụng Bđt Cauchy và Bunhiacopxki :
\(a+3b=2b+\left(a+b\right)\ge2\sqrt[]{2b\left(a+b\right)}\)
\(ab+bc+ca\le\sqrt[]{\left(a^2+b^2+c^2\right)\left(a^2+b^2+c^2\right)}=a^2+b^2+c^2\)

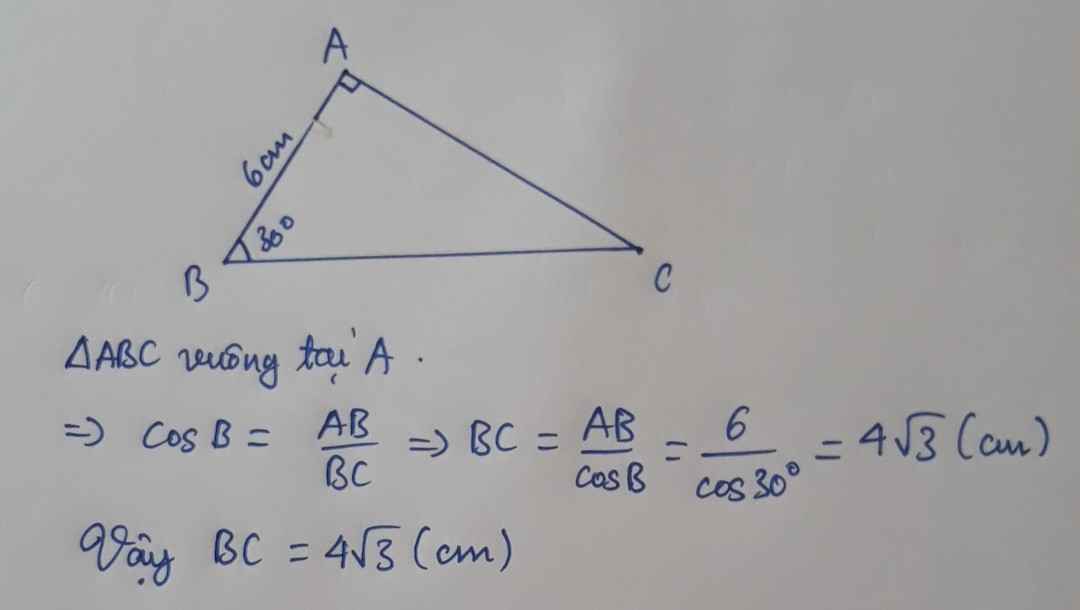
xét ΔABC vuông tại A có \(cosB=\dfrac{AB}{BC}\)
=>\(\dfrac{6}{BC}=cos30=\dfrac{\sqrt{3}}{2}\)
=>\(BC=6\cdot\dfrac{2}{\sqrt{3}}=4\sqrt{3}\left(cm\right)\)

\(\left|A+B\right|< =\left|A\right|+\left|B\right|\)
=>\(\left(\left|A+B\right|\right)^2< =\left(\left|A\right|+\left|B\right|\right)^2\)
=>\(A^2+B^2+2AB< =A^2+B^2+2\left|AB\right|\)
=>2AB<=2|AB|
=>AB<=|AB|(luôn đúng)
Dấu '=' xảy ra khi AB>=0

Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)
=>\(\dfrac{6}{BC}=sin30=\dfrac{1}{2}\)
=>\(BC=6\cdot2=12\left(cm\right)\)
a: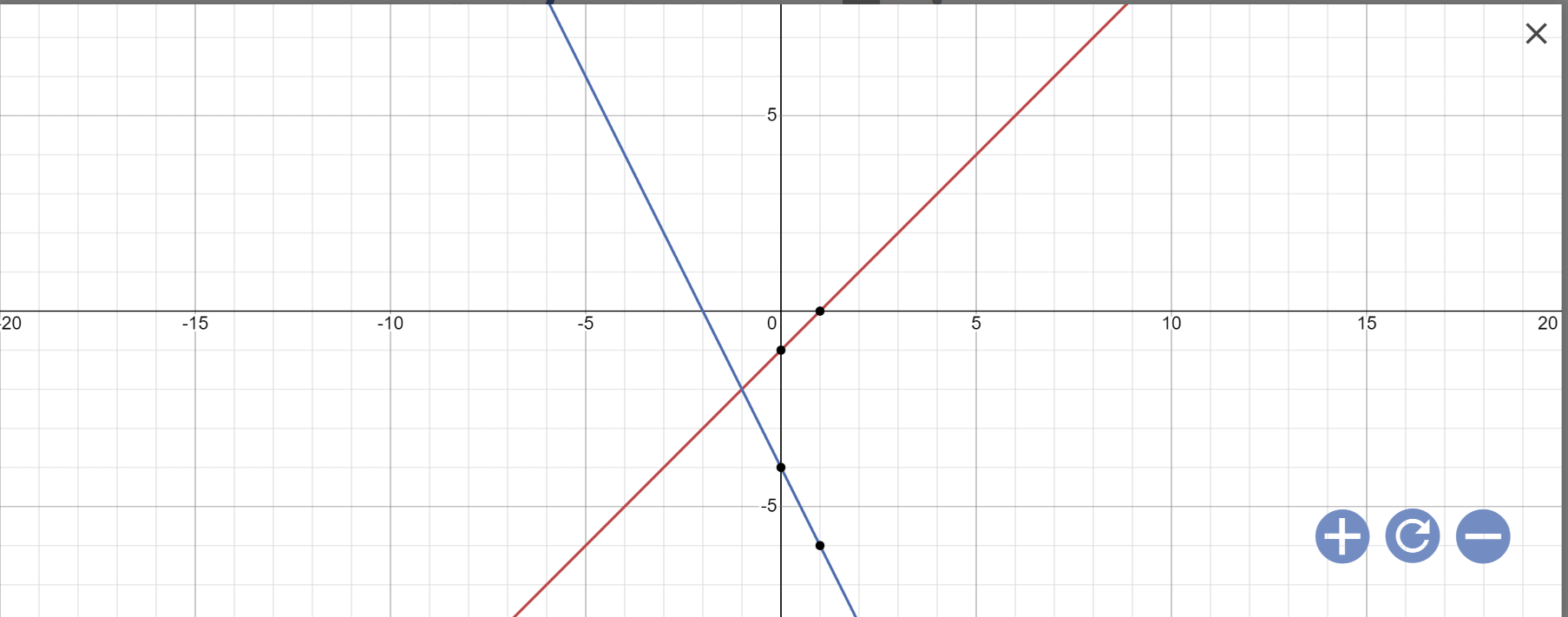
b: Phương trình hoành độ giao điểm là:
-2x-4=x-1
=>-2x-x=-1+4
=>-3x=3
=>x=-1
Thay x=-1 vào y=x-1, ta được:
y=-1-1=-2
Vậy: Tọa độ giao điểm là A(-1;-2)