Lời giải:

Gọi số lọ sát khuẩn 2 lớp điều chế được ngày thứ nhất lần lượt là $a,b$. Theo bài ra ta có:

$a+b=110$

$1,25a+1,2b=135$
Giải hệ phương trình gồm 2 PT trên thu được: $a=60; b=50$ (lọ)

số tự nhiên bé nhất mà lập phương số đó có $4$ chữ số cuối bên phải là chữ số $3$ là số: 17

là số 17

\(\dfrac{25112012}{11}=2282911-\dfrac{9}{11}\Rightarrow a=2282911\)

\(\dfrac{9}{11}=\dfrac{1}{\dfrac{11}{9}}=\dfrac{1}{1+\dfrac{2}{9}}=\dfrac{1}{1+\dfrac{1}{\dfrac{9}{2}}}=\dfrac{1}{1+\dfrac{1}{4+\dfrac{1}{2}}}\)

\(\Rightarrow b=1;c=4;d=2\)

Sao lại là toán lớp 9 hả bạn???

Đây là toán lớp 9 mà bạn?

Áp dụng BĐT AM-GM ta có 

x^3/1+y +1+y/4+1/2 >= 3 căn 3(x^3/8) =3x/2

Tương tự: y^3/1+z + 1+z/4 +1/2 >= 3z/2

z^3/1+x +1+x/4 + 1/2 >= 3z/2

=> P + x+y+z+3/4 +3/2 >= 3(x+y+z)/2

<=> P >= [5(x+y+z)-3]/4 -3/2

<=> P >= 5(x+y+z)/4 -9/4

Mặt khác x+y+z>=xy+yz+zx>=3

( bạn tự chứng minh nhé)

=> P>= 15/4 -9/4=3/2

=>P >=3/2

Dấu = xảy ra khi x=y=z=1 

Nhớ tick cho mình nhé

Áp dụng BĐT AM-GM ta có 

x^3/1+y +1+y/4+1/2 >= 3 căn 3(x^3/8) =3x/2

Tương tự: y^3/1+z + 1+z/4 +1/2 >= 3z/2

z^3/1+x +1+x/4 + 1/2 >= 3z/2

=> P + x+y+z+3/4 +3/2 >= 3(x+y+z)/2

<=> P >= [5(x+y+z)-3]/4 -3/2

<=> P >= 5(x+y+z)/4 -9/4

Mặt khác x+y+z>=xy+yz+zx>=3

( bạn tự chứng minh nhé)

=> P>= 15/4 -9/4=3/2

=>P >=3/2

Dấu = xảy ra khi x=y=z=1 

Nhớ tick cho mình nhé

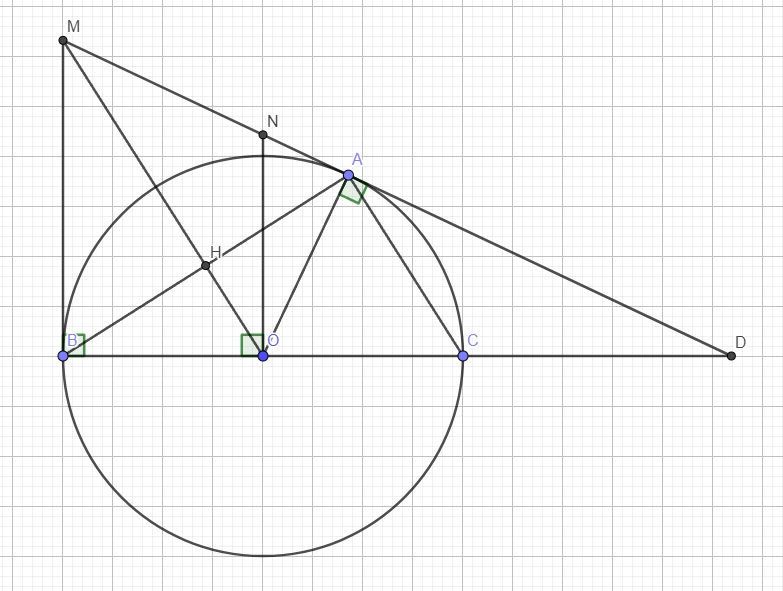
4c.

Do M là giao điểm 2 tiếp tuyến tại A và B, theo tính chất hai tiếp tuyến cắt nhau 

\(\Rightarrow\widehat{OMN}=\widehat{OMB}\)

Mà \(MB||NO\) (cùng vuông góc BC) \(\Rightarrow\widehat{OMB}=\widehat{MON}\) (so le trong)

\(\Rightarrow\widehat{OMN}=\widehat{MON}\)

\(\Rightarrow\Delta OMN\) cân tại N

\(\Rightarrow MN=ON\)

Cũng theo 2 t/c 2 tiếp tuyến cắt nhau \(\Rightarrow MA=MB\)

Do MD là tiếp tuyến của (O) tại A \(\Rightarrow OA\perp MD\)

Áp dụng hệ thức lượng trong tam giác vuông OND với đường cao OA:

\(ON^2=NA.ND\Rightarrow MN^2=NA.ND\)

\(\Rightarrow MN^2=\left(MA-MN\right).ND=\left(MB-MN\right).ND\)

\(\Rightarrow MN^2=MB.ND-MN.ND\)

\(\Rightarrow MB.ND-MN^2=MN.ND\)

\(\Rightarrow\dfrac{MB.ND-MN^2}{MN.ND}=1\)

\(\Rightarrow\dfrac{MB}{MN}-\dfrac{MN}{ND}=1\) (đpcm)

Công thức: 

ĐK:x≥1. Chứng minh y≥0

trải lời đi nhanh lên