Ta có:  1; 2; 3; 4..; 1999; 2022

Dãy số trên từ 1 đến 1999 là dãy số cách đều với khoảng cách là:

     2 - 1   = 1

Tại sao 2022 lại không theo quy luật đó

           2022 - 1999 = 2

Đề bài em chép đã đúng chưa?

Câu 1:

a: \(k=\dfrac{y}{x}=\dfrac{3}{5}\)

b: \(\dfrac{y}{x}=\dfrac{3}{5}\)

=>\(y=\dfrac{3}{5}x\)

c: Thay x=-5 vào \(y=\dfrac{3}{5}x\), ta được:

\(y=\dfrac{3}{5}\cdot\left(-5\right)=-3\)

Thay x=15 vào \(y=\dfrac{3}{5}x\), ta được:

\(y=\dfrac{3}{5}\cdot15=9\)

Câu 4: Gọi khối lượng giấy vụn ba chi đội 7A,7B,7C thu được lần lượt là a(kg),b(kg),c(kg)

(Điều kiện:a>0; b>0; c>0)

Khối lượng giấy vụn của ba đội thu được lần lượt tỉ lệ với 9;7;8

=>\(\dfrac{a}{9}=\dfrac{b}{7}=\dfrac{c}{8}\)

Tổng khối lượng là 120kg nên a+b+c=120

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{9}=\dfrac{b}{7}=\dfrac{c}{8}=\dfrac{a+b+c}{9+7+8}=\dfrac{120}{24}=5\)

=>\(a=5\cdot9=45;b=7\cdot5=35;c=8\cdot5=40\)

vậy: Gọi khối lượng giấy vụn ba chi đội 7A,7B,7C thu được lần lượt là 45(kg),35(kg),40(kg)

\(\dfrac{9}{14}\) : \(\dfrac{5}{7}\) - \(\dfrac{5}{6}\) 

= \(\dfrac{9}{14}\) x \(\dfrac{7}{5}\) - \(\dfrac{5}{6}\)

= \(\dfrac{9}{10}\) - \(\dfrac{5}{6}\)

= \(\dfrac{1}{15}\)

\(\dfrac{9}{14}:\dfrac{5}{7}-\dfrac{5}{6}\)

\(=\dfrac{9}{14}\times\dfrac{7}{5}-\dfrac{5}{6}\)

\(=\dfrac{9}{10}-\dfrac{5}{6}\)

\(=\dfrac{27}{30}-\dfrac{25}{30}=\dfrac{2}{30}=\dfrac{1}{15}\)

SỐ LỚN NHẤT CÓ 2 CHỮ SỐ CÓ HIỆU 2 CHỮ SỐ BẰNG 8 LÀ: 91

SỐ NHỎ NHẤT CÓ 2 CHỮ SỐ MÀ TỔNG CỦA 2 CHỮ SỐ BẰNG 7 LÀ :16

HIỆU 2 SỐ LÀ:

91 - 16= 75

                 ĐÁP SỐ:75

                 Giải:

+ Để được số lớn nhất có hai chữ số thì chữ số hàng chục phải lớn nhất có thể nên chữ số hàng chục là 9

 Hiệu hai chữ số là 8 nên chữ số hàng đơn vị là:

             9 - 8 = 1

Số lớn nhất có hai chữ số mà hiệu hai chữ số bằng 8 là số 91

Vậy số bị trừ là 91

+ Để được số nhỏ nhất có hai chữ số thì chữ số hàng cao phải nhỏ nhất có thể nên chữ số hàng chục là 1

Vì tổng hai chữ số bằng 7 nên chữ số hàng đơn vị là: 

              7 - 1 = 6

Số nhỏ nhất có hai chữ số mà tổng hai chữ số bằng 7 là 16.

Vậy số trừ là 16

Hiệu của hai số đó là: 

               91 - 16 = 75

Đáp số: 75 

\(\dfrac{1}{6}\) + \(\dfrac{1}{12}\) + \(\dfrac{1}{20}\) + .. + \(\dfrac{1}{90}\) = \(\dfrac{6}{y}\)

\(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\)+ ... + \(\dfrac{1}{9.10}\) = \(\dfrac{6}{y}\)

\(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}-\dfrac{1}{5}\) + .. + \(\dfrac{1}{9}-\dfrac{1}{10}\) = \(\dfrac{6}{y}\)

\(\dfrac{1}{2}\) - \(\dfrac{1}{10}\) = \(\dfrac{6}{y}\) 

\(\dfrac{2}{5}\) = \(\dfrac{6}{y}\) 

  y = 6 : \(\dfrac{2}{5}\) 

y = 15

\(\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{90}=\dfrac{6}{y}\)

=>\(\dfrac{6}{y}=\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+...+\dfrac{1}{9\times10}\)

=>\(\dfrac{6}{y}=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\)

=>\(\dfrac{6}{y}=\dfrac{1}{2}-\dfrac{1}{10}=\dfrac{5}{10}-\dfrac{1}{10}=\dfrac{4}{10}=\dfrac{2}{5}\)

=>\(y=5\times\dfrac{6}{2}=15\)

\(36\cdot25+35\cdot50-6\cdot25\)

\(=25\cdot\left(36-6\right)+35\cdot50\)

\(=25\cdot30+35\cdot2\cdot25\)

\(=25\cdot\left(30+70\right)=25\cdot100=2500\)

   36 x 25  + 35 x 50 - 6 x 25

= 36 x 25 + 35 x 50 - 6 x 25

= 36 x 25 + 35 x 2 x 25  - 6 x 25

= 25 x (36  + 35 x 2 - 6)

= 25 x (36 + 70 - 6)

= 25 x (36 - 6 + 70)

= 25 x (30 + 70)

= 25 x 100

= 2500 

Ta có: \(\left(x-3\right)\left(x-1\right)-x\left(2-x\right)=0\)

=>\(x^2-4x+3-2x+x^2=0\)

=>\(2x^2-6x+3=0\)

=>\(x^2-3x+\dfrac{3}{2}=0\)

=>\(x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}-\dfrac{9}{4}+\dfrac{3}{2}=0\)

=>\(\left(x-\dfrac{3}{2}\right)^2-\dfrac{3}{4}=0\)

=>\(\left(x-\dfrac{3}{2}\right)^2=\dfrac{3}{4}\)

=>\(\left[{}\begin{matrix}x-\dfrac{3}{2}=\dfrac{\sqrt{3}}{2}\\x-\dfrac{3}{2}=-\dfrac{\sqrt{3}}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{3}}{2}\\x=\dfrac{3-\sqrt{3}}{2}\end{matrix}\right.\)

a: Ta có: mn//xy

=>\(\widehat{mAB}=\widehat{ABy}\)(hai góc so le trong)

=>\(\widehat{mAB}=60^0\)

b:

Ta có: \(\widehat{yBc}+\widehat{yBA}=180^0\)(hai góc kề bù)

=>\(\widehat{yBc}=180^0-60^0=120^0\)

Bz là phân giác của góc yBc

=>\(\widehat{yBz}=\widehat{cBz}=\dfrac{\widehat{yBc}}{2}=\dfrac{120^0}{2}=60^0\)

Ta có: \(\widehat{nAB}+\widehat{mAB}=180^0\)(hai góc kề bù)

=>\(\widehat{nAB}=180^0-60^0=120^0\)

At là phân giác của góc nAB

=>\(\widehat{nAt}=\widehat{tAB}=\dfrac{\widehat{nAB}}{2}=\dfrac{120^0}{2}=60^0\)

Ta có: \(\widehat{ABz}=\widehat{ABy}+\widehat{yBz}=60^0+60^0=120^0\)

Ta có: \(\widehat{ABz}+\widehat{BAt}=120^0+60^0=180^0\)

mà hai góc này là hai góc ở vị trí trong cùng phía

nên At//Bz

                   Bài 1:

B = \(x^2\) - 2\(xy\) + 2y² 

Thay \(x=13\) và y = 3 vào B ta được

B = 13² - 2.13.3 + 2.3²

B = 169 - 26.3 + 2.9

B = 169 - 78 + 18

B = 91 + 18

B = 109 

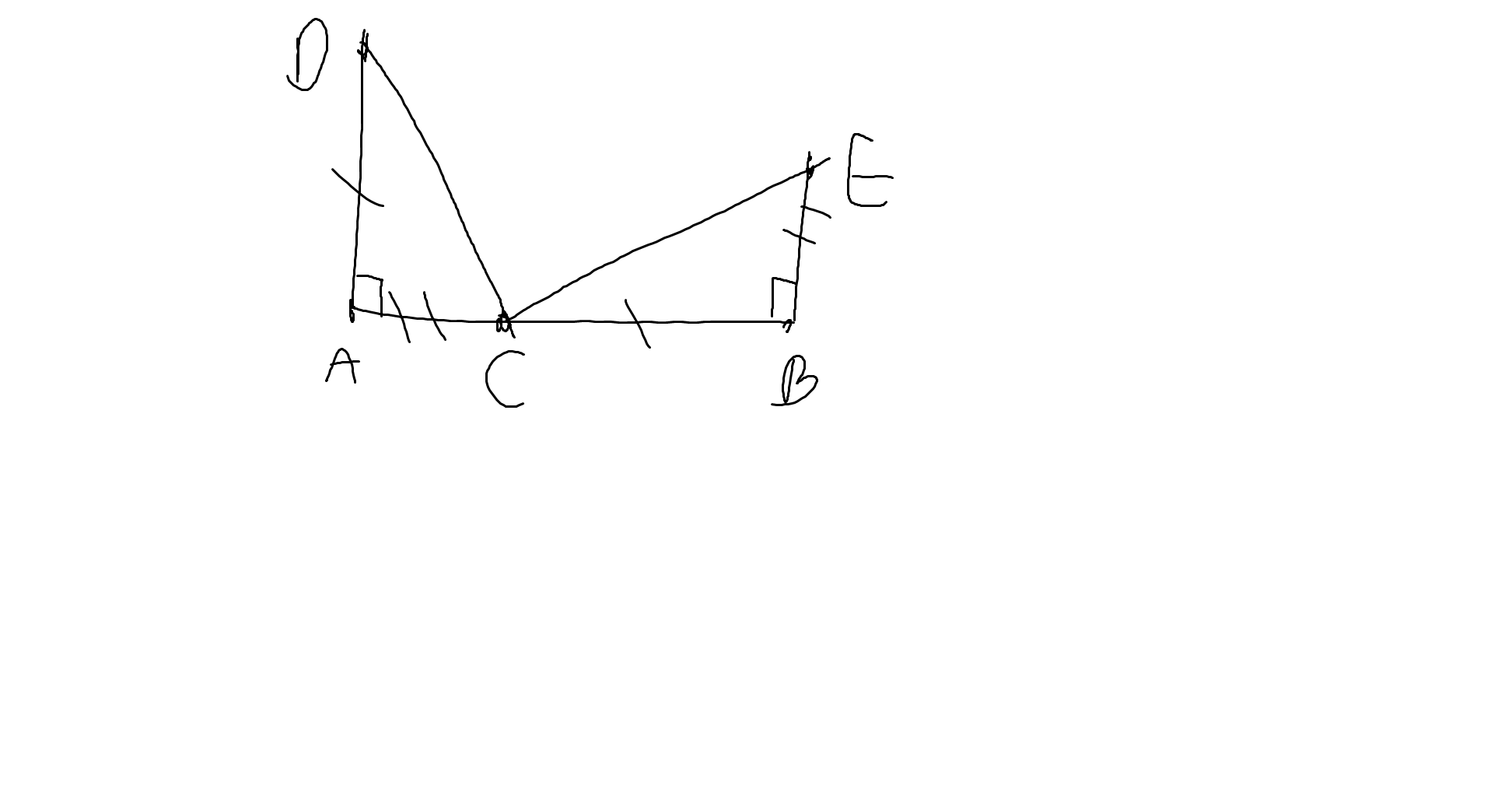
a: Xét ΔDAC vuông tại A và ΔCBE vuông tại B có

DA=CB

AC=BE

Do đó: ΔDAC=ΔCBE

b: ΔDAC=ΔCBE

=>\(\widehat{DCA}=\widehat{CEB}\)

=>\(\widehat{DCA}+\widehat{ECB}=90^0\)

Ta có: \(\widehat{DCA}+\widehat{ECB}+\widehat{DCE}=180^0\)

=>\(\widehat{DCE}+90^0=180^0\)

=>\(\widehat{DCE}=90^0\)

=>CD\(\perp\)CE