a) Chứng minh: ΔMKD ΔAHD và MK. AD = AH. DM.

Ta có: ∠MKD = ∠AHD (cùng chéo với ∠MAD)
Và ∠KMD = ∠HAD (cùng chéo với ∠MAD)
Do đó, ΔMKD ΔAHD (theo góc góc)
Từ đó, ta có: MK/HA = MD/HD (theo định lý hình giống)
Sắp xếp lại, ta được: MK. AD = AH. DM.

b) Chứng minh SMBC/SABC=MD/AB

Đầu tiên, ta chứng minh ΔBMD ~ ΔABC. Ta có ∠BMD = ∠BAC (cùng chéo với ∠BAM) và ∠BDM = ∠BCA (cùng chéo với ∠BMA). Do đó, ΔBMD ~ ΔABC theo nguyên lý góc - góc.

Vì ΔBMD ~ ΔABC, ta có MD/AB = BD/BC = BM/AC. Sắp xếp lại, ta được MD/AB = S_BMD/S_ABC.

Tương tự, ta cũng có ΔCMD ~ ΔABC và MD/AB = S_CMD/S_ABC.

Do đó, MD/AB = (S_BMD + S_CMD)/S_ABC = S_BMC/S_ABC = S_ABC/S_ABC = 1.

Vậy, ta đã chứng minh được SMBC/SABC = MD/AB.

Không biết có đúng không nhỉ?

a: Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{5}{7}\)

Xét ΔDMB vuông tại M và ΔDNC vuông tại N có

\(\widehat{MDB}=\widehat{NDC}\)(hai góc đối đỉnh)

Do đó: ΔDMB~ΔDNC

=>\(\dfrac{BM}{CN}=\dfrac{DB}{DC}=\dfrac{5}{7}=\dfrac{MB}{NC}\)

b:

Xét ΔAMB vuông tại M và ΔANC vuông tại N có

\(\widehat{BAM}=\widehat{CAN}\)

Do đó:ΔAMB~ΔANC

=>\(\dfrac{AM}{AN}=\dfrac{AB}{AC}\)

mà \(\dfrac{AB}{AC}=\dfrac{DB}{DC}=\dfrac{DM}{DN}\)

nên \(\dfrac{AM}{AN}=\dfrac{DM}{DN}\)

=>\(AM\cdot DN=AN\cdot DM\)

c: ΔAMB~ΔANC

=>\(\dfrac{S_{AMB}}{S_{ANC}}=\left(\dfrac{AB}{AC}\right)^2=\dfrac{25}{49}\)

a: Xét ΔCHA vuông tại H và ΔCIH vuông tại I có

\(\widehat{HCA}\) chung

Do đó: ΔCHA~ΔCIH

=>\(\dfrac{CH}{CI}=\dfrac{HA}{IH}\)

=>\(\dfrac{CH}{HA}=\dfrac{CI}{IH}\)

b: O ở đâu vậy bạn?

Lời giải:
Với $x,y$ nguyên thì $2x^2+2y^2-4xy+2x-2y$ là 1 số chẵn. Mà $1$ là số lẻ nên không tồn tại $x,y$ nguyên thỏa mãn đề bài.

a:

  b:

  c:

a=2,b=4

Để giải phương trình này, ta có thể sử dụng một số phân tích như sau:
1. Trường hợp đặc biệt: Nếu (a = b), thì phương trình trở thành (a^a = a^a), điều này luôn đúng với mọi giá trị của (a).
2. Trường hợp (a = 1) hoặc (b = 1): Nếu một trong hai số là 1, thì phương trình trở thành (1^b = b^1), điều này cũng luôn đúng với mọi giá trị của (b).
3. Trường hợp (a = 2) và (b = 4): Ta thấy rằng (2^4 = 4^2), vậy đây là một giá trị thỏa mãn.
4. Trường hợp (a = 4) và (b = 2): Ta thấy rằng (4^2 = 2^4), vậy đây cũng là một giá trị thỏa mãn.
Vậy, các cặp giá trị thỏa mãn phương trình là ((a, b) = (2, 4)) và ((a, b) = (4, 2)).

a) Thay tọa độ điểm M(1; 4) vào (d), ta có:

(-2m + 1).1 + m - 3 = 4

-2m + 1 + m - 3 = 4

-2m - 2 = 4

-m = 4 + 2

-m = 6

m = -6

b) m = -6

(d): y = 13x - 9

Bảng giá trị:

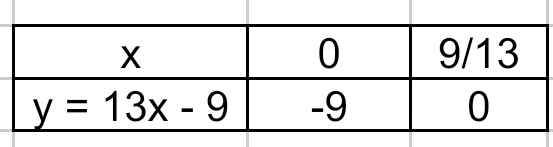
Đồ thị:

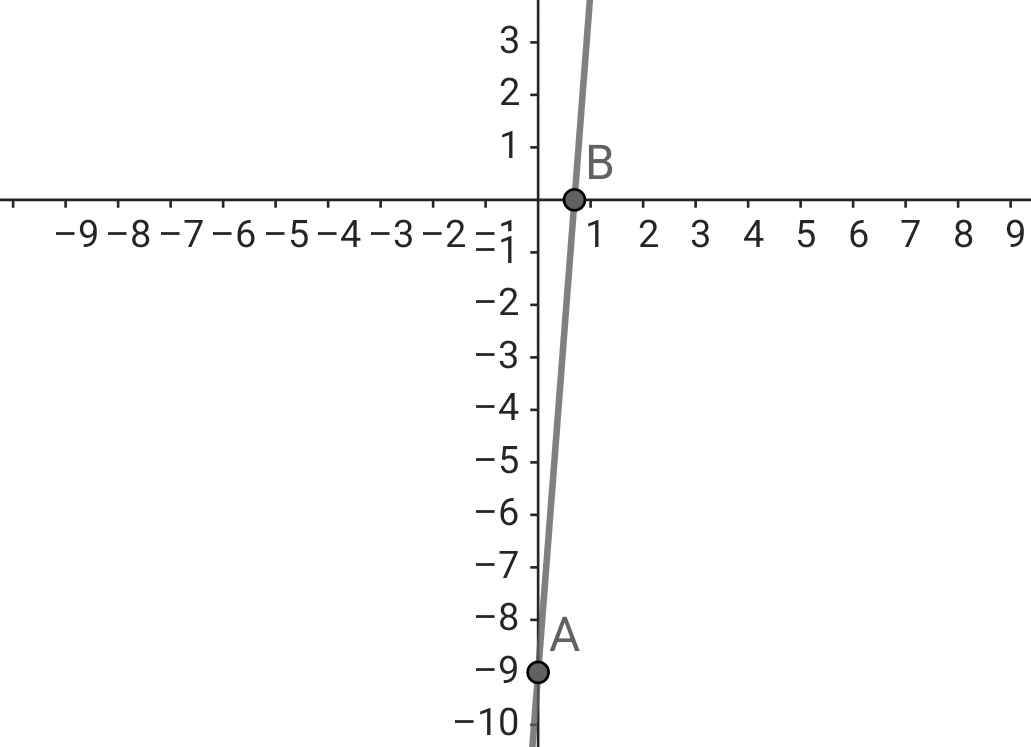
a; 

Để d đi qua điểm A(1; 4)

Thì tọa độ điểm A phải thỏa mãn phương trình đường thẳng d

Thay tọa độ điểm A vào phương trình đường thẳng d ta có:

     (-2m + 1).\(1\) + m - 3  = 4

       -2m + 1  + m -  3 = 4

       -m - 2 = 4

        m = - 2 - 6

        m = - 8

   Olm chào em, lần sau em chụp ảnh câu hỏi vào đây để olm dễ check lại em nhé. Cảm ơn em đã tin tưởng và sử dụng olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm.