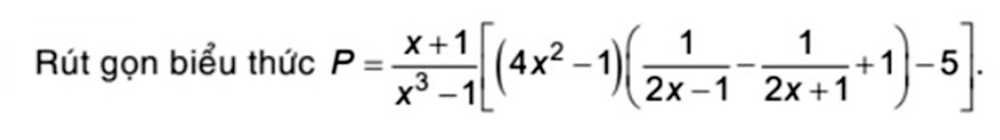Cho hàm số y = -2 x + 4 và điểm A 3,2 B 3,2 C 1,2 bằng phương pháp vẽ đồ thị xác định các điểm A B C có gốc đồ thị hàm số đã cho không
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để đồ thị hàm số y=(3-m)x+3m+2 song song với đường thẳng y=5x-4 thì \(\left\{{}\begin{matrix}3-m=5\\3m+2\ne-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=3-5=-2\\3m\ne-6\end{matrix}\right.\)
=>\(m\in\varnothing\)

\(f\left(x\right)=\left(x^2-3x+3\right)\left(x^2-2x+3\right)-2x^2\)
\(=\left(x^2-2x+3-x\right)\left(x^2-2x+3\right)-2x^2\)
\(=\left(x^2-2x+3\right)^2-x\left(x^2-2x+3\right)-2x^2\)
\(=\left(x^2-x+3-2x\right)\left(x^2-x+3+x\right)\)
\(=\left(x^2-4x+3\right)\left(x^2+3\right)\)
Đặt f(x)=0
=>\(\left(x^2-4x+3\right)\left(x^2+3\right)=0\)
mà \(x^2+3>0\forall x\)
nên \(x^2-4x+3=0\)
=>(x-1)(x-3)=0
=>\(\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)

Bài 2:
a: Khi x=4 thì \(M=\dfrac{4+3}{4-2}=\dfrac{7}{2}\)
b: \(M=\dfrac{2}{3}\)
=>\(\dfrac{x+3}{x-2}=\dfrac{2}{3}\)
=>3(x+3)=2(x-2)
=>3x+9=2x-4
=>3x-2x=-4-9
=>x=-13(nhận)
c: Để M là số nguyên dương thì \(\left\{{}\begin{matrix}x+3⋮x-2\\M>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2+5⋮x-2\\\dfrac{x+3}{x-2}>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5⋮x-2\\\left[{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2\in\left\{1;-1;5;-5\right\}\\\left[{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\end{matrix}\right.\)
=>\(x\in\left\{3;7\right\}\)
Bài 3:
ΔMIN vuông tại I
=>\(IM^2+IN^2=MN^2\)
=>\(x=MI=\sqrt{12^2-5^2}=\sqrt{144-25}=\sqrt{119}\left(cm\right)\)
ΔMIP vuông tại I
=>\(IM^2+IP^2=PM^2\)
=>\(y=\sqrt{119+100}=\sqrt{219}\left(cm\right)\)
Bài 4:
a: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔBAC~ΔBHA
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{HAB}\right)\)
Do đó: ΔHBA~ΔHAC
=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)
=>\(HA^2=HB\cdot HC\)
c: Xét tứ giác AIHK có \(\widehat{AIH}=\widehat{AKH}=\widehat{KAI}=90^0\)
nên AIHK là hình chữ nhật
=>\(\widehat{AKI}=\widehat{AHI}\)
mà \(\widehat{AHI}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AKI}=\widehat{ABC}\)
ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}\)
\(\widehat{AKI}+\widehat{MAC}=\widehat{ABC}+\widehat{ACB}=90^0\)
=>AM\(\perp\)IK

\(x^2-5x+3=0\\ \Delta=b^2-4ac=\left(-5\right)^2-4\cdot1\cdot3=13>0\\ x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-5\right)-\sqrt{13}}{2\cdot1}=\dfrac{5-\sqrt{13}}{2}\\ x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(-5\right)+\sqrt{13}}{2\cdot1}=\dfrac{5+\sqrt{13}}{2}\\ \text{vậy phương trình có 2 nghiệm là }x_1=\dfrac{5-\sqrt{13}}{2};x_2=\dfrac{5+\sqrt{13}}{2}\)

\(\left(x^2-y^2\right)^2+4x^2y^2+x^2-2y^2=0\)
\(\Rightarrow x^4+y^4-2x^2y^2+4x^2y^2+x^2-2y^2=0\)
\(\Rightarrow x^4+y^4+2x^2y^2+x^2-2y^2=0\)
\(\Rightarrow\left(x^2+y^2\right)^2-2\left(x^2+y^2\right)+3x^2=0\)
\(\Leftrightarrow\left(x^2+y^2-1\right)^2=1-3x^2\le1\)
\(\Rightarrow-1\le x^2+y^2-1\le1\)
\(\Rightarrow0\le x^2+y^2\le2\)
\(\Rightarrow A_{min}=0\) khi \(x=y=0\)
\(A_{max}=2\) khi \(x=0;y=\pm\sqrt{2}\)

\(P=\dfrac{x+1}{x^3-1}\left[\left(4x^2-1\right)\left(\dfrac{1}{2x-1}-\dfrac{1}{2x+1}+1\right)-5\right]\)
\(=\dfrac{x+1}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\left[\left(2x-1\right)\left(2x+1\right)\cdot\dfrac{2x+1-2x+1+4x^2-1}{\left(2x-1\right)\left(2x+1\right)}-5\right]\)
\(=\dfrac{x+1}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\left(4x^2+1-5\right)\)
\(=\dfrac{x+1}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\left(4x^2-4\right)\)
\(=\dfrac{x+1}{\left(x-1\right)\left(x^2+x+1\right)}\cdot4\left(x-1\right)\left(x+1\right)\)
\(=\dfrac{4\left(x+1\right)^2}{x^2+x+1}\)