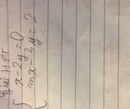
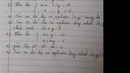
P/s: lần sau đăng hẳn câu hỏi lên đừng có kiểu đăng như thế này, không ai muốn làm đâu

Bài này sai ngay từ đầu rồi-.-

Bài làm:

Ta có: \(x^2+\frac{1}{x^2}=7\Leftrightarrow\left(x+\frac{1}{x}\right)^2-2\cdot x\cdot\frac{1}{x}=7\)

\(\Leftrightarrow\left(x+\frac{1}{x}\right)^2-2=7\Leftrightarrow\left(x+\frac{1}{x}\right)^2=9\)

\(\Rightarrow x+\frac{1}{x}=3\left(x>0\right)\)

Bây giờ thì dùng tam giác Pascal mà khai triển ra thôi

\(\left(x+\frac{1}{x}\right)^5=x^5+5x^4\cdot\frac{1}{x}+10x^3\cdot\frac{1}{x^2}+10x^2\cdot\frac{1}{x^3}+5x\cdot\frac{1}{x^4}+\frac{1}{x^5}\)

\(=x^5+5x^3+10x+\frac{10}{x}+\frac{5}{x^3}+\frac{1}{x^5}=\left(x^5+\frac{1}{x^5}\right)+5\left(x^3+\frac{1}{x^3}\right)+10\left(x+\frac{1}{x}\right)\)

\(\Rightarrow x^5+\frac{1}{x^5}=\left(x+\frac{1}{x}\right)^5-5\left(x^3+\frac{1}{x^3}\right)-10\left(x+\frac{1}{x}\right)\)

\(=3^5-5\left(x+\frac{1}{x}\right)\left(x^2-x\cdot\frac{1}{x}+\frac{1}{x^2}\right)-10\cdot3\)

\(=243-5\cdot3\cdot\left(7-1\right)-30=123\)

Vậy \(x^5+\frac{1}{x^5}=123\)

Đáp án là  720 .

Nếu số P \(⋮\)2016 thì số P \(⋮\)3  vì 2016 \(⋮\)3.

Tổng các chữ số của P là 5050 \(⋮̸\)3 .

\(\Rightarrow\)(đpcm)

\(ĐK:x\inℝ\)

\(\sqrt[3]{2x+3}+1=x^3+3x^2+2x\Leftrightarrow\sqrt[3]{2x+3}=x^3+3x^2+2x-1\)\(\Leftrightarrow2x+3=\left(x^3+3x^2+2x-1\right)^3\)\(\Leftrightarrow\left(x+2\right)\left(x^2+x-1\right)\left(x^6+6x^5+14x^4+14x^3+4x^2-x+2\right)=0\)

Dễ dàng kiểm tra \(x^6+6x^5+14x^4+14x^3+4x^2-x+2\)không thể phân tích thành nhân tử với các hệ số nguyên nên không có nghiệm nguyên và hữu tỉ

\(\Rightarrow x\in\left\{-2;\frac{\sqrt{5}-1}{2};\frac{-1-\sqrt{5}}{2}\right\}\)

Thử lại ta thấy ba giá trị trên đều thỏa mãn phương trình

Vậy tập nghiệm của phương trình \(S=\left\{\frac{\pm\sqrt{5}-1}{2};-2\right\}\)

a) Phương trình \(x^2-2mx-2m-1=0\)có các hệ số a = 1; b = - 2m; c = - 2m - 1

\(\Delta=\left(-2m\right)^2-4\left(-2m-1\right)=4m^2+8m+4=4\left(m+1\right)^2\ge0\forall m\)

Vậy phương trình luôn có 2 nghiệm x₁, x₂ với mọi m (đpcm)

b) Theo Viète, ta có: \(x_1+x_2=2m;x_1x_2=-2m-1\)

Hệ thức \(\frac{x_1}{x_2}+\frac{x_2}{x_1}=\frac{-5}{2}\Leftrightarrow2\left(x_1^2+x_2^2\right)=-5x_1x_2\)

\(\Leftrightarrow2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=-5x_1x_2\)hay \(2\left(4m^2+4m+2\right)=10m+5\Leftrightarrow8m^2-2m-1=0\)\(\Leftrightarrow\orbr{\begin{cases}m=\frac{1}{2}\\m=-\frac{1}{4}\end{cases}}\)

Vậy \(m=\frac{1}{2}\)hoặc \(m=-\frac{1}{4}\)thì phương trình có 2 nghiệm x₁, x₂ thỏa mãn\(\frac{x_1}{x_2}+\frac{x_2}{x_1}=\frac{-5}{2}\)

\(P=\frac{1}{\sqrt{a+3}}+\frac{1}{\sqrt{b+3}}\ge\frac{\left(1+1\right)^2}{\sqrt{a+3}+\sqrt{b+3}}=\frac{4}{\sqrt{a+3}+\sqrt{b+3}}\)

Ta có: 

\(\left(\sqrt{a+3}.1+\sqrt{b+3}.1\right)^2\le\left(1^2+1^2\right)\left(a+3+b+3\right)\le16\)

\(\Rightarrow\sqrt{a+3}+\sqrt{b+3}\le\sqrt{16}=4\)

\(\Rightarrow P\ge\frac{4}{\sqrt{a+3}+\sqrt{b+3}}\ge\frac{4}{4}=1\).

Dấu \(=\)xảy ra khi \(a=b=1\).

\(P=\frac{1}{\sqrt{a+3}}+\frac{1}{\sqrt{b+3}}\Rightarrow P^2=\left(\frac{1}{a+3}+\frac{1}{b+3}\right)+\frac{2}{\sqrt{\left(a+3\right)\left(b+3\right)}}\)\(\ge\frac{4}{\left(a+b\right)+6}+\frac{2}{\frac{\left(a+3\right)+\left(b+3\right)}{2}}=\frac{8}{a+b+6}\ge\frac{8}{2+6}=1\)

\(\Rightarrow P\ge1\)

Đẳng thức xảy ra khi a = b = 1

Ta có A = 5x² - 2xy + 2y² - 4x + 2y + 3

=> 2A = 10x² - 4xy + 4y² - 8x + 4y + 6

= (x² - 4xy + 4y²) - 2(x - 2y) + 1 + 9x² - 6x + 1 + 4

= \(\left(x-2y\right)^2-2\left(x-2y\right)+1+9\left(x^2-\frac{2}{3}x+\frac{1}{9}\right)+4\)

\(=\left(x-2y-1\right)^2+9\left(x-\frac{1}{3}\right)^2+4\)\(\ge4\)

=> A \(\ge\)2 

Dấu "=" xảy ra <=> \(\hept{\begin{cases}x-2y-=0\\x-\frac{1}{3}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x-2y=1\\x=\frac{1}{3}\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-\frac{1}{3}\\x=\frac{1}{3}\end{cases}}\)

Vậy khi x = 1/3 ; y = -1/3 thì A đạt GTNN

\(A=5x^2+2y^2-2xy-4x+2y\)\(+3\)

\(=\left(x^2-2xy+y^2\right)+\)\(\left(4x^2-4x+1\right)+\)\(\left(y^2+2y+1\right)+1\)

\(Tacó\)