Question 15. Last year, Phuc participated in _______ funds for street children.
A. raising B. making C. gathering D. taking
Question 16. Classical music is not _______ modern music.
A. as popular as B. popular than C. more popular D. as popular than
Question 17. She feels itchy and her nose is running. She says she has ________.
A. headache B. toothache C. allergy D. flu
Question 18. Will you _______ making models in the future?
A. pick up B. look for C. take up D. find

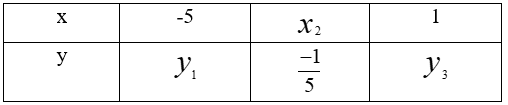
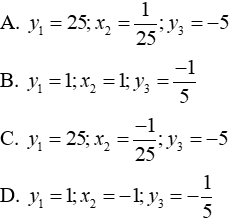
15. A
16. A
17. D
18. C
15.A
16.A
17.D
18.C
HT