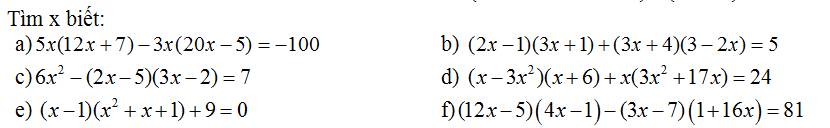4,096 : 16 = 0,256.

32,55 : 1,5 = 21,7.

13,57 : 4,9 = 2,769387755 (Số j to dã man).

13,57: 4,9 dư nhiều lắm

cụ thể: 2,7693877551020408163265306122448979591836734

hơi dài nên thông cảm(có đáp án là đc rồi, đòi hỏi nhìu)

Tổng vận tốc hai xe là 34+50=84(km/h)

Hai xe gặp nhau sau khi đi được: 126:84=1,5(giờ)=1h30p

Hai người gặp nhau lúc:

7h+1h30p=8h30p

Chỗ gặp nhau cách A:

1,5x50=75(km)

số đó là 6.267+5=1607 ạ

a: AD là phân giác của góc BAC

=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{\widehat{BAC}}{2}=30^0\)

Xét ΔADB có \(\widehat{ADB}+\widehat{BAD}+\widehat{ABD}=180^0\)

=>\(\widehat{ADB}+30^0+80^0=180^0\)

=>\(\widehat{ADB}=70^0\)

b: Xét ΔABD có \(\widehat{BAD}< \widehat{ADB}< \widehat{ABD}\)
mà BD,AB,AD lần lượt là các cạnh đối diện của các góc BAD,ADB,ABD

nên BD<AB<AD

c: Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)

=>\(\widehat{ACB}+60^0+80^0=180^0\)

=>\(\widehat{ACB}=40^0\)

ta có: \(\widehat{ADB}+\widehat{ADC}=180^0\)

=>\(\widehat{ADC}+70^0=180^0\)

=>\(\widehat{ADC}=110^0\)

Xét ΔADC có \(\widehat{DAC}< \widehat{DCA}< \widehat{ADC}\)

mà DC,DA,AC lần lượt là cạnh đối diện của các góc DAC,DCA,ADC

nên DC<DA<AC

Giúp đang cần gấp

4/6 + 7/13 + 17/9 + 19/18 + 1/9 + 14/6

= (4/6 + 14/6) + (17/9 + 1/9) + 19/18 + 7/13

= 3 + 2 + 19/18 + 7/13

= 5 + 19/18 + 7/13

= 109/18 + 7/13

= 1543/234

a: \(5x\left(12x+7\right)-3x\left(20x-5\right)=-100\)

=>\(60x^2+35x-60x^2+15x=-100\)

=>50x=-100

=>x=-2

b: \(\left(2x-1\right)\left(3x+1\right)+\left(3x+4\right)\left(3-2x\right)=5\)

=>\(6x^2+2x-3x-1+9x-6x^2+12-8x=5\)

=>11=5(loại)

c: \(6x^2-\left(2x-5\right)\left(3x-2\right)=7\)

=>\(6x^2-\left(6x^2-4x-15x+10\right)=7\)

=>19x-10=7

=>19x=17

=>\(x=\dfrac{17}{19}\)

d: \(\left(x-3x^2\right)\left(x+6\right)+x\left(3x^2+17x\right)=24\)

=>\(x^2+6x-3x^3-18x^2+3x^3+17x^2=24\)

=>6x=24

=>x=4

e: \(\left(x-1\right)\left(x^2+x+1\right)+9=0\)

=>\(x^3-1+9=0\)

=>\(x^3+8=0\)

=>\(x^3=-8\)

=>x=-2

f: \(\left(12x-5\right)\left(4x-1\right)-\left(3x-7\right)\left(16x+1\right)=81\)

=>\(48x^2-12x-20x+5-\left(48x^2+3x-112x-7\right)=81\)

=>-32x+5+109x+7=81

=>77x=81-12=69

=>\(x=\dfrac{69}{77}\)

1/3 + 13/19 - 4/9 + 6/19 + 5/18

= (13/19 + 6/19) - (1/3 + 4/9) + 5/18

= 1 - 7/9 + 5/18

= 1 - 14/18 + 5/18

= 13/18 + 5/18

= 1

'

Gọi d=ƯCLN(3n+1;4n+1)

=>\(\left\{{}\begin{matrix}3n+1⋮d\\4n+1⋮d\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}12n+4⋮d\\12n+3⋮d\end{matrix}\right.\)

=>\(12n+4-12n-3⋮d\)

=>\(1⋮d\)

=>d=1

=>ƯCLN(4n+1;3n+1)=1

=>\(\dfrac{3n+1}{4n+1}\) là phân số tối giản