$2,5 - 3x = 5,5 .2022^0$
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A. $x = \dfrac{-9}{4}$ B. $x = \dfrac{-15}{4}$ C. $x = \dfrac{15}{4}$ D. $x = \dfrac{9}{4}$

a: Vì O thuộc tia đối của tia AB
nên A nằm giữa O và B
=>OB=OA+AB=4+6=10(cm)
M là trung điểm của OA
=>\(OM=MA=\dfrac{OA}{2}=\dfrac{4}{2}=2\left(cm\right)\)
N là trung điểm của OB
=>\(ON=NB=\dfrac{OB}{2}=5\left(cm\right)\)
Vì OM<ON
nên M nằm giữa O và N
=>OM+MN=ON
=>MN+2=5
=>MN=3(cm)
b: \(MN=ON-OM=\dfrac{OB-OA}{2}=\dfrac{BA}{2}\)
=>MN không phụ thuộc vào điểm O
c: Gọi số điểm phải lấy thêm là n(điểm)
Tổng số điểm trên đoạn thẳng AB lúc này là n+2(điểm)
Số tam giác tạo thành là \(C^2_{n+2}\left(tamgiác\right)\)
Theo đề, ta có: \(C^2_{n+2}=465\)
=>\(\dfrac{\left(n+2\right)!}{\left(n+2-2\right)!\cdot2!}=465\)
=>(n+1)(n+2)=930
=>\(n^2+3n-928=0\)
=>\(\left[{}\begin{matrix}n=29\left(nhận\right)\\n=-32\left(loại\right)\end{matrix}\right.\)
Vậy: Số điểm phải lấy thêm là 29 điểm

a: \(-1,2+\dfrac{2}{3}+x=5\)
=>\(x=5+1,2-\dfrac{2}{3}=6,2-\dfrac{2}{3}\)
=>\(x=\dfrac{31}{5}-\dfrac{2}{3}=\dfrac{93}{15}-\dfrac{10}{15}=\dfrac{83}{15}\)
b: \(2\dfrac{4}{7}-3x=\dfrac{-4}{5}+\dfrac{2}{3}\)
=>\(\dfrac{18}{7}-3x=\dfrac{-12}{15}+\dfrac{10}{15}=\dfrac{-2}{15}\)
=>\(3x=\dfrac{18}{7}+\dfrac{2}{15}=\dfrac{270}{105}+\dfrac{14}{105}=\dfrac{284}{105}\)
=>\(x=\dfrac{284}{315}\)
c: \(\dfrac{1}{6}-\dfrac{3}{8}+1,75=3\dfrac{4}{3}-x\)
=>\(\dfrac{13}{3}-x=\dfrac{4}{24}-\dfrac{9}{24}+\dfrac{42}{24}=\dfrac{37}{24}\)
=>\(x=\dfrac{13}{3}-\dfrac{37}{24}=\dfrac{108}{24}-\dfrac{37}{24}=\dfrac{71}{24}\)
d: \(\dfrac{1}{6}-\dfrac{4}{9}+0,125=2\dfrac{4}{3}-2x\)
=>\(\dfrac{10}{3}-2x=\dfrac{-11}{72}\)
=>\(2x=\dfrac{10}{3}+\dfrac{11}{72}=\dfrac{240}{72}+\dfrac{11}{72}=\dfrac{251}{72}\)
=>\(x=\dfrac{251}{144}\)
e: \(2\dfrac{2}{3}-4x=\dfrac{-7}{5}+\dfrac{2}{3}\)
=>\(2+\dfrac{2}{3}-4x=\dfrac{-7}{5}+\dfrac{2}{3}\)
=>\(2-4x=-\dfrac{7}{5}\)
=>\(4x=2+\dfrac{7}{5}=\dfrac{17}{5}\)
=>\(x=\dfrac{17}{20}\)
f: \(\dfrac{1}{2}-\left(x+\dfrac{1}{3}\right)=\dfrac{5}{6}\)
=>\(x+\dfrac{1}{3}=\dfrac{1}{2}-\dfrac{5}{6}=\dfrac{3}{6}-\dfrac{5}{6}=\dfrac{-2}{6}=-\dfrac{1}{3}\)
=>\(x=-\dfrac{1}{3}-\dfrac{1}{3}=-\dfrac{2}{3}\)
g: \(\left(\dfrac{3}{5}-\dfrac{4}{3}\right)+\left(\dfrac{5}{8}-x\right)=\dfrac{9}{7}\)
=>\(\dfrac{-11}{15}+\dfrac{5}{8}-x=\dfrac{9}{7}\)
=>\(\dfrac{-13}{120}-x=\dfrac{9}{7}\)
=>\(x=-\dfrac{13}{120}-\dfrac{9}{7}=\dfrac{-1171}{840}\)
a, \(-1,2+\dfrac{2}{3}+x=5\Leftrightarrow x=5+1,2-\dfrac{2}{3}=\dfrac{83}{15}\)
b, \(2\dfrac{4}{7}-3x=-\dfrac{4}{5}+\dfrac{2}{3}\Leftrightarrow\dfrac{18}{7}-3x=-\dfrac{2}{15}\Leftrightarrow3x=\dfrac{284}{105}\Leftrightarrow x=\dfrac{284}{315}\)
c, \(\dfrac{1}{6}-\dfrac{3}{8}+1,75=3\dfrac{4}{3}-x\Leftrightarrow-x+\dfrac{13}{3}=\dfrac{37}{24}\Leftrightarrow x=\dfrac{13}{3}-\dfrac{37}{24}=\dfrac{67}{24}\)
d, \(\dfrac{1}{6}-\dfrac{4}{9}+0,125=2\dfrac{4}{3}-2x\Leftrightarrow-2x+\dfrac{10}{3}=-\dfrac{-11}{72}\Leftrightarrow2x=\dfrac{251}{72}\Leftrightarrow x=\dfrac{251}{144}\)
e, \(2\dfrac{2}{3}-4x=-\dfrac{7}{5}+\dfrac{2}{7}\Leftrightarrow\dfrac{8}{3}-4x=-\dfrac{39}{35}\Leftrightarrow4x=\dfrac{397}{105}\Leftrightarrow x=\dfrac{397}{420}\)
f, \(\dfrac{1}{2}-\left(x+\dfrac{1}{3}\right)=\dfrac{5}{6}\Leftrightarrow x+\dfrac{1}{3}=\dfrac{1}{2}-\dfrac{5}{6}=-\dfrac{1}{3}\Leftrightarrow x=-\dfrac{2}{3}\)
g, \(\left(\dfrac{3}{5}-\dfrac{4}{3}\right)+\left(\dfrac{5}{8}-x\right)=\dfrac{9}{7}\Leftrightarrow\dfrac{-11}{15}+\dfrac{5}{8}-x=\dfrac{9}{7}\Leftrightarrow\left(-\dfrac{13}{120}\right)-x=\dfrac{9}{7}\Leftrightarrow x=-\dfrac{1171}{840}\)

a) \(\dfrac{-3}{100}>\dfrac{-50}{100}=-\dfrac{1}{2}\)
\(\dfrac{-2}{3}< \dfrac{-1,5}{3}=-\dfrac{1}{2}\)
\(\Rightarrow\dfrac{-3}{100}>\dfrac{-2}{3}\)
b) \(\dfrac{-3}{5}=\dfrac{-9}{15}\)
\(\dfrac{-2}{3}=\dfrac{-10}{15}\)
Mà: - 9 > -10
\(\Rightarrow-\dfrac{9}{15}>\dfrac{-10}{15}\)
hay `-3/5>-2/3`
c) \(\dfrac{-5}{4}< \dfrac{-2}{4}=-\dfrac{1}{2}\)
\(-\dfrac{3}{8}>\dfrac{-4}{8}=-\dfrac{1}{2}\)
\(\Rightarrow-\dfrac{5}{4}< \dfrac{-3}{8}\)
d) \(-\dfrac{2}{3}=\dfrac{1}{3}-1\)
\(-\dfrac{3}{4}=\dfrac{1}{4}-1\)
Vì: `1/3>1/4`
`=>1/3-1>1/4-1`
Hay `-2/3>-3/4`
a: \(\dfrac{-3}{100}=\dfrac{-3\cdot3}{100\cdot3}=\dfrac{-9}{300};\dfrac{2}{-3}=\dfrac{-2}{3}=\dfrac{-2\cdot100}{3\cdot100}=\dfrac{-200}{300}\)
mà -9>-200
nên \(\dfrac{-3}{100}>\dfrac{-2}{3}\)
b: \(\dfrac{-3}{5}=\dfrac{-3\cdot3}{5\cdot3}=\dfrac{-9}{15};\dfrac{2}{-3}=\dfrac{-2}{3}=\dfrac{-2\cdot5}{3\cdot5}=\dfrac{-10}{15}\)
mà -9>-10
nên \(\dfrac{-3}{5}>\dfrac{2}{-3}\)
c: \(\dfrac{-5}{4}=\dfrac{-5\cdot2}{4\cdot2}=\dfrac{-10}{8};\dfrac{-3}{8}=\dfrac{-3}{8}\)
mà -10<-3
nên \(-\dfrac{5}{4}< -\dfrac{3}{8}\)
d: \(\dfrac{-2}{3}=\dfrac{-2\cdot4}{3\cdot4}=\dfrac{-8}{12};\dfrac{3}{-4}=\dfrac{-3}{4}=\dfrac{-3\cdot3}{4\cdot3}=\dfrac{-9}{12}\)
mà -8>-9
nên \(-\dfrac{2}{3}>\dfrac{3}{-4}\)
e: \(\dfrac{267}{-268}=\dfrac{-267}{268}>-1;-1=\dfrac{-1343}{1343}>\dfrac{-1347}{1343}\)
Do đó: \(\dfrac{267}{-268}>\dfrac{-1347}{1343}\)
f: \(\dfrac{2022\cdot2023-1}{2022\cdot2023}=1-\dfrac{1}{2022\cdot2023}\)
\(\dfrac{2023\cdot2024-1}{2023\cdot2024}=1-\dfrac{1}{2023\cdot2024}\)
Ta có: 2022<2024
=>\(2022\cdot2023< 2023\cdot2024\)
=>\(\dfrac{1}{2022\cdot2023}>\dfrac{1}{2023\cdot2024}\)
=>\(-\dfrac{1}{2022\cdot2023}< -\dfrac{1}{2023\cdot2024}\)
=>\(\dfrac{-1}{2022\cdot2023}+1< \dfrac{-1}{2023\cdot2024}+1\)
=>\(\dfrac{2022\cdot2023-1}{2022\cdot2023}< \dfrac{2023\cdot2024-1}{2023\cdot2024}\)
g: \(\dfrac{2022\cdot2023}{2022\cdot2023+1}=1-\dfrac{1}{2022\cdot2023+1}\)
\(\dfrac{2023\cdot2024}{2023\cdot2024+1}=1-\dfrac{1}{2023\cdot2024+1}\)
Vì \(2022\cdot2023+1< 2023\cdot2024+1\)
nên \(\dfrac{1}{2022\cdot2023+1}>\dfrac{1}{2023\cdot2024+1}\)
=>\(\dfrac{-1}{2022\cdot2023+1}< \dfrac{-1}{2023\cdot2024+1}\)
=>\(\dfrac{-1}{2022\cdot2023+1}+1< \dfrac{-1}{2023\cdot2024}+1\)
=>\(\dfrac{2022\cdot2023}{2022\cdot2023+1}< \dfrac{2023\cdot2024}{2023\cdot2024+1}\)

\(B=7-\left|4x-3\right|\)
Ta có: \(\left|4x-3\right|\ge0\forall x\)
\(\Rightarrow B=7-\left|4x-3\right|\le7-0=7\forall x\)
Dấu "=" xảy ra khi: \(4x-3=0\Leftrightarrow x=\dfrac{3}{4}\)
Vậy: ...

\(4^{x+2}.3^x=16.12^5\\ \Rightarrow4^{x+2}.3^x=4^2.4^5.3^5\\ \Rightarrow4^{x+2}.3^x=4^7.3^5\\ \Rightarrow\dfrac{4^{x+2}}{4^7}.\dfrac{3^x}{3^5}=1\\ \Rightarrow4^{x-5}.3^{x-5}=1\\ \Rightarrow12^{x-5}=1\\ \Rightarrow x-5=0\\ \Rightarrow x=5\)
\(4^{x+2}\cdot3^x=16\cdot12^5\)
\(\Rightarrow4^{x+2}\cdot3^x=4^2\cdot4^5\cdot3^5\)
\(\Rightarrow4^{x+2}\cdot3^x=4^7\cdot3^5\)
\(\Rightarrow\left\{{}\begin{matrix}4^{x+2}=4^7\\3^x=3^5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+2=7\\x=5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=5\\x=5\end{matrix}\right.\)
\(\Rightarrow x=5\)
Vậy: ...

\(B=\left(1-\dfrac{1}{2}\right)\cdot\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{n+1}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{n}{n+1}\)
\(=\dfrac{1}{n+1}\)

8. Ta có:
\(x=\dfrac{2a-1}{a}=\dfrac{2a}{a}-\dfrac{1}{a}=2-\dfrac{1}{a}\)
Vì 2 ∈ Z nên x thuộc Z khi \(\dfrac{1}{a}\) thuộc Z
⇒ 1 ⋮ a ⇒ a ∈ Ư(1) = {1; -1}
Vậy: ...
 i am oke am fine kìn chái nà :,)SOS
i am oke am fine kìn chái nà :,)SOS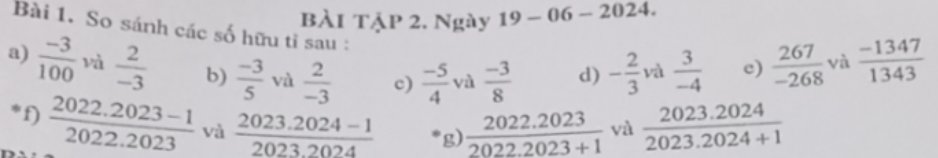

\(2,5-3x=5,5.2022^0\)
\(=>2,5-3x=5,5.1\)
\(=>2,5-3x=5,5\)
\(=>3x=2,5-5,5\)
\(=>3x=-3\)
\(=>x=\left(-3\right):3\)
\(=>x=\dfrac{-3}{3}=-1\)
Vậy...
\(#NqHahh\)
\(2,5-3x=5,5\cdot2022^0\)
\(2,5-3x=5,5\cdot1\)
\(2,5-3x=5,5\)
\(3x=2,5-5,5\)
\(3x=-3\)
\(x=-3:3\)
\(x=-1\)
Vậy \(x=-1\)