Từ điểm M nằm ngoài (O) kẻ các tiếp tuyến MA,MB đến (O)(A,B là các tiếp điểm) và cát tuyến MCD sao cho MC<MD và tia MC nằm giữa 2 tia MA, MO. Gọi H là giao của MO và AB. Kẻ đường thẳng song song với AD cắt AM tại I; cắt AB tại K. CMR: C là trung điểm của IK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)0,6.a
b)\(a^2\).(a-3)
c)36.(a-1)
d)\(\dfrac{1.a^2}{a-b}\).(a-b)

a)\(\sqrt{7.63}\)=21
b)\(\sqrt{2,5.30.48}\)=60
c)\(\sqrt{0,4.6,4}\)=1,6
d)\(\sqrt{2,7.5.1,5}\)=4,5

a, \(\sqrt{0.09\cdot64=\sqrt{0.09}\cdot\sqrt{64}=0.3\cdot8=2.4}\)
b, \(\sqrt{2^4\cdot\left(-7\right)^2}=\sqrt{16\cdot49}=\sqrt{16}\cdot\sqrt{49}=4\cdot7=28\)
c, \(\sqrt{121\cdot360}=\sqrt{121\cdot36}=\sqrt{121}\cdot\sqrt{36}=11\cdot6=66\)
d, \(\sqrt{2^2\cdot3^4}=\sqrt{2^2}\cdot\sqrt{3^4}=2\cdot3^2=18\)
a)\(\sqrt{0,09}.\sqrt{64}\)=0,3.8=2,4
b)\(\sqrt{2^4}.\sqrt{\left(-7\right)^2}\)=4.7=28
c)\(\sqrt{121.36}\)=\(\sqrt{121}.\sqrt{36}\)=11.6=66
d)\(\sqrt{2^2}.\sqrt{3^4}\)=2.9=18

a) Δ' = b'2 - ac = [-(n-1)]2 - 2n + 3
= n2 - 2n + 1 - 2n + 3
= n2 - 4n + 4 = ( n - 2 )2 ≥ 0 ∀ n
hay pt luôn có nghiệm ∀ n (đpcm)
b) Theo Viète ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2n-2\\x_1x_2=\frac{c}{a}=2n-3\end{cases}}\)
Khi đó P = x12 + x22 = ( x1 + x2 )2 - 2x1x2
= ( 2n - 2 )2 - 2( 2n - 3 )
= 4n2 - 8n + 4 - 4n + 6
= 4n2 - 12n + 10
= ( 2n - 3 )2 + 1 ≥ 1 ∀ n
Dấu "=" xảy ra <=> n = 3/2 . Vậy MinP = 1

\(\sqrt{x+17}+\sqrt{x}=17\left(ĐK:x\ge0\right)\)
\(\Leftrightarrow\left(\sqrt{x+17}-9\right)+\left(\sqrt{x}-8\right)=0\)
\(\Leftrightarrow\frac{x+17-81}{\sqrt{x+17}+9}+\frac{x-64}{\sqrt{x}+8}=0\)
\(\Leftrightarrow\left(x-64\right)\left(\frac{1}{\sqrt{x+17}+9}+\frac{1}{\sqrt{x}+8}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=64\left(tm\right)\\\frac{1}{\sqrt{x+17}+9}+\frac{1}{\sqrt{x}+8}=0\left(1\right)\end{cases}}\)
Vì \(x\ge0\Rightarrow\hept{\begin{cases}\sqrt{x+17}+9>0\\\sqrt{x}+8>0\end{cases}}\)
\(\Rightarrow VT_{\left(1\right)}>0\)
\(\Rightarrow pt\left(1\right)\)vô nghiệm.
Vậy pt có nghiệm x=64

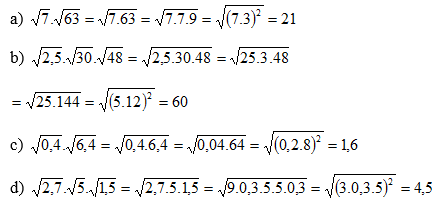
giúp mk vs ạ mk đg cần gấp