Bài 21 (trang 111 SGK Toán 9 Tập 1)
Cho tam giác $ABC$ có $AB = 3$, $AC = 4$, $BC = 5$. Vẽ đường tròn $(B; BA)$. Chứng minh rằng $AC$ là tiếp tuyến của đường tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=\sqrt{64}=8\left(cm\right)\)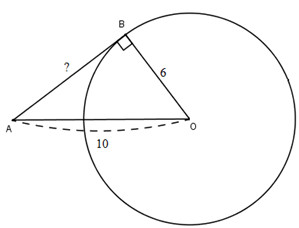
Áp dụng định lý Pytago vào tam giác AOB vuông tại B, ta có:
AB=\(\sqrt{AO^2-OB^2}=\sqrt{10^2-6^2}\)\(=\sqrt{64}=8\left(cm\right)\)

a) vẽ bạn tự vẽ nha
b) Xét pt hoành độ giao điểm chung của (d) và (P) ta có:
\(\frac{1}{4}x^2=x+m\)
\(\Leftrightarrow x^2-4x-4m=0\left(1\right)\)
\(\Delta^,=4+4m\)
Để (d) tiếp xúc với (P) \(\Leftrightarrow\Delta^,=0\)
\(\Leftrightarrow4+4m=0\)
\(\Leftrightarrow m=-1\)
Thay m=-1 vào pt (1) ta được :
\(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x=2\)
\(\Rightarrow y=\frac{1}{4}.2^2=1\)
Gọi tọa độ tiếp điểm của (d) tiếp xúc với (P) là A(x,y)
=> tọa độ tiếp điểm là \(A\left(2;1\right)\)

Gọi O là tâm của một đường tròn bất kì có bán kính bằng 1cm và tiếp xúc với đường thẳng xy.
Ta có: R = 1, và đường tròn tiếp xúc với đường thẳng xy nên ta có: d = R, suy ra d = 1.
=> Tâm O cách đường thẳng xy một khoảng cố định 1cm nên nằm trên các đường thẳng (a) và (b) song song với xy và cách xy một khoảng là 1cm.
Gọi OO là tâm của một đường tròn bất kì có bán kính bằng 1 cm và tiếp xúc với đường thẳng x yxy. Khi đó khoảng cách từ OO đến đường thẳng x yxy là 1cm. Tâm OO cách đường thẳng xyxy cố định 1cm nên nằm trên hai đường thẳng mm và m'm′ song song với xyxy và cách xyxy là 1cm.

Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.

| R | d | Vị trí tương đối |
| 5 cm | 3cm | Cắt nhau tại 2 điểm phân biệt trên đường tròn |
| 6cm | 6cm | Tiếp xúc nhau |
| 4cm | 7cm | Không giao nhau |

a) đk: \(\hept{\begin{cases}x\ge0\\x\ne1\end{cases}}\)
\(M=\frac{x}{\sqrt{x}-1}\cdot\left(\frac{4}{\sqrt{x}+2}-\frac{\sqrt{x}-6}{x+2\sqrt{x}}\right)\)
\(M=\frac{x}{\sqrt{x}-1}\cdot\frac{4\sqrt{x}-\sqrt{x}+6}{\left(\sqrt{x}+2\right)\sqrt{x}}\)
\(M=\frac{x}{\sqrt{x}-1}\cdot\frac{3\sqrt{x}+6}{\left(\sqrt{x}+2\right)\sqrt{x}}\)
\(M=\frac{x}{\sqrt{x}-1}\cdot\frac{3\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\sqrt{x}}\)
\(M=\frac{3\sqrt{x}}{\sqrt{x}-1}\)
b) Nếu \(\sqrt{x}-1< 0\Rightarrow M< 0\)
Nếu \(\sqrt{x}-1>0\Rightarrow M>0\) nên TH này thỏa mãn
Với \(\sqrt{x}-1>0\Leftrightarrow\sqrt{x}>1\Rightarrow x>1\)
\(M=\frac{3\sqrt{x}}{\sqrt{x}-1}=\frac{3\left(\sqrt{x}-1\right)+3}{\sqrt{x}-1}=3+\frac{3}{\sqrt{x}-1}\)
Để M lớn nhất => \(\frac{3}{\sqrt{x}-1}\)max => \(\sqrt{x}-1\) min
...

\(x^2-2x+m-3=0\)
\(\Delta=4-4m+12\)
Để pt có 2 no \(x_1,x_2\Leftrightarrow\Delta\ge0\)
\(\Leftrightarrow16-4m\ge0\)
\(\Leftrightarrow m\le4\)
Theo hệ thức Vi-et ta có:
\(\hept{\begin{cases}x_1+x_2=2\left(1\right)\\x_1.x_2=m-3\left(2\right)\end{cases}}\)
\(x_1^2+3x_2^2=4x_1x_2\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(x_1-3x_2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x_1=x_2\\x_1=3x_2\end{cases}}\)
TH1: \(x_1=x_2\)
Kết hợp với (1)
\(\Rightarrow x_1=x_2=1\)
Thay \(x_1=x_2=1\)vào (2) ta được :
\(m-3=1\)
\(\Leftrightarrow m=4\left(tm\right)\)
TH2: \(x_1=3x_2\)
kết hợp với (1)
\(\Rightarrow\hept{\begin{cases}x_1+x_2=2\\x_1=3x_2\end{cases}}\Leftrightarrow\hept{\begin{cases}x_1=\frac{3}{2}\\x_2=\frac{1}{2}\end{cases}}\)
Thay \(\hept{\begin{cases}x_1=\frac{3}{2}\\x_2=\frac{1}{2}\end{cases}}\)vào (2) ta được:
\(\frac{3}{4}=m-3\)
\(\Leftrightarrow m=\frac{15}{4}\left(tm\right)\)
Vậy \(m\in\left\{4;\frac{15}{4}\right\}\)thì pt có no \(x_1,x_2\)thỏa mãn \(x_1^2+3x_2^2=4x_1x_2\)
Tam giác ABCABC có:
AB^2+AC^2=3^{2}+4^{2}=5^{2}AB2+AC2=32+42=52
Mặt khác: BC^{2}=5^{2}BC2=52
Vậy \mathrm{AB}^{2}+\mathrm{AC}^{2}=\mathrm{BC}^{2}AB2+AC2=BC2.
Do đó \widehat{BAC}=90^{\circ}BAC=90∘ (định lí Py-ta-go đảo).
CACA vuông góc với bán kính BABA tại AA nên CACA là tiếp tuyến của đường tròn (B)(B).
tam giác ABC