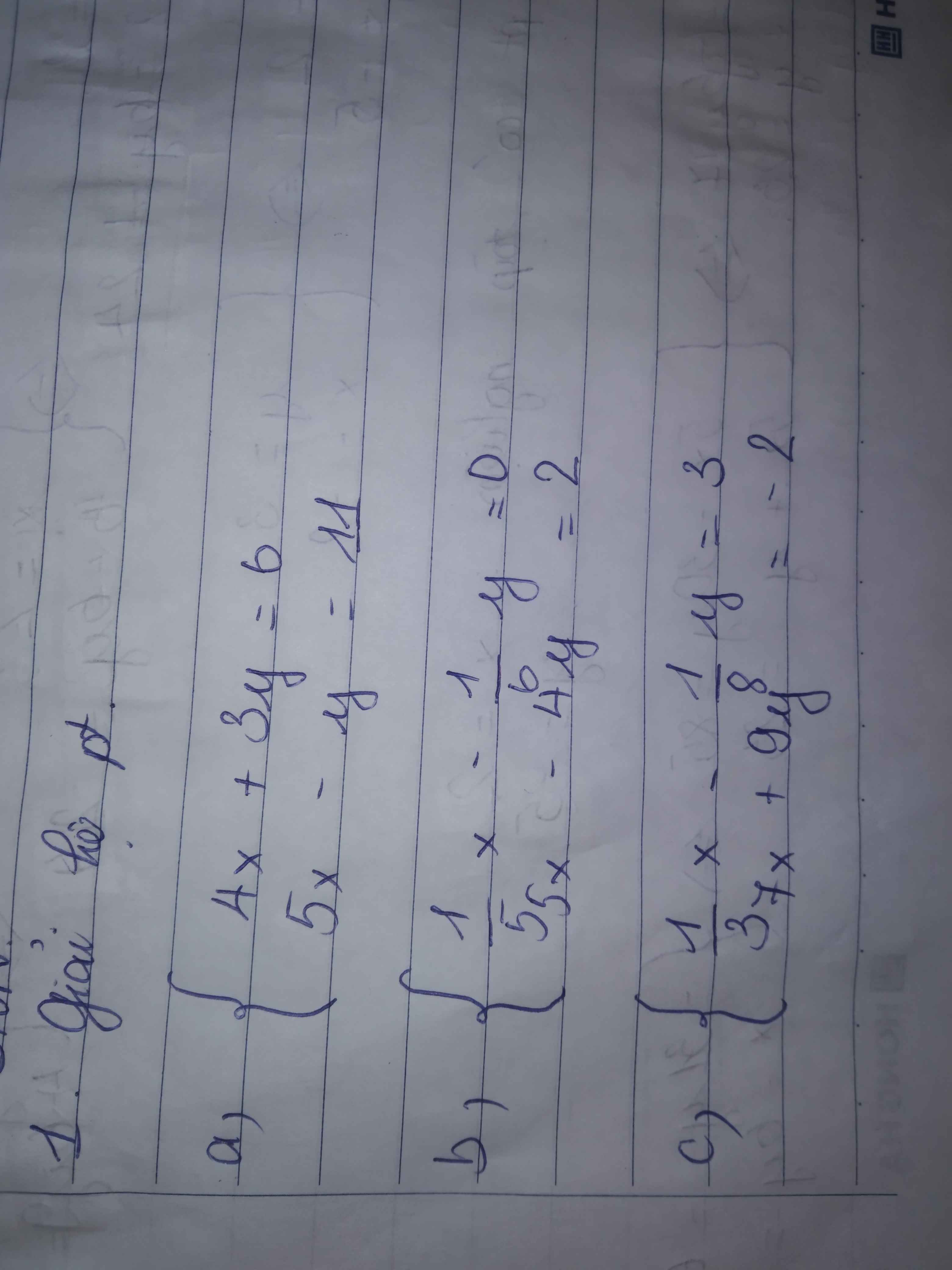
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\left\{{}\begin{matrix}4x+3y=6\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\15x-3y=33\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+3y+15x-3y=6+33\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19x=39\\y=5x-11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{39}{19}\\y=5\cdot\dfrac{39}{19}-11=-\dfrac{14}{19}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{1}{5}x-\dfrac{1}{6}y=0\\5x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=\dfrac{y}{6}\\5x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\5\cdot\dfrac{5}{6}y-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{25}{6}y-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{1}{6}y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\x=\dfrac{5}{6}\cdot12=10\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{1}{3}x-\dfrac{1}{8}y=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}-\dfrac{y}{8}=3\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8x-3y}{24}=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x-3y=72\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}24x-9y=216\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x-9y+7x+9y=216-2\\8x-3y=72\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}31x=214\\3y=8x-72\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{214}{31}\\y=\dfrac{8x-72}{3}=\dfrac{-520}{93}\end{matrix}\right.\)

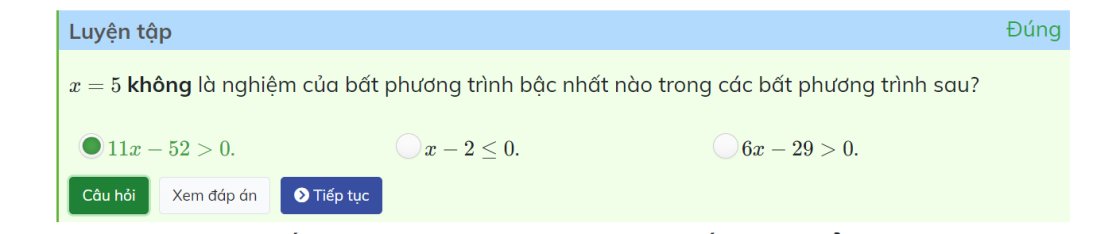
Khi x=5 thì \(11x-52=11\cdot5-52=55-52=3>0\)
=>Đúng
Khi x=5 thì \(6x-29=6\cdot5-29=30-29=1>0\)
=>6x-29>0 đúng
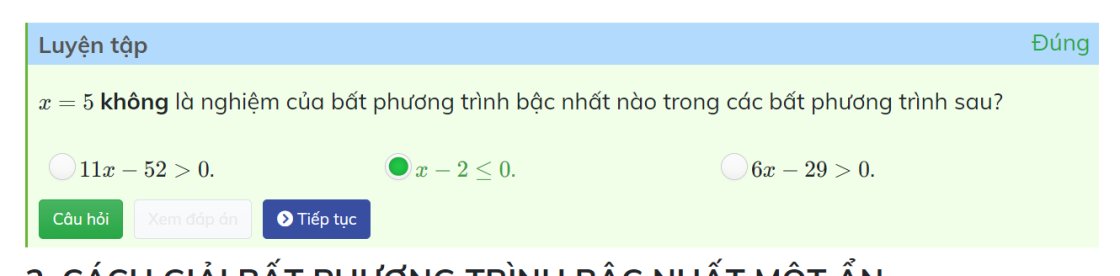
Khi x=5 thì 5-2=3<=0(sai)
=>x-2<=0 là đáp án sai duy nhất, hai cái còn lại đúng

a: \(\left\{{}\begin{matrix}4x+3y=6\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\15x-3y=33\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+3y+15x-3y=6+33\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19x=39\\y=5x-11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{39}{19}\\y=5\cdot\dfrac{39}{19}-11=-\dfrac{14}{19}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{1}{5}x-\dfrac{1}{6}y=0\\5x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=\dfrac{y}{6}\\5x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\5\cdot\dfrac{5}{6}y-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{25}{6}y-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{1}{6}y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\x=\dfrac{5}{6}\cdot12=10\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{1}{3}x-\dfrac{1}{8}y=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}-\dfrac{y}{8}=3\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8x-3y}{24}=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x-3y=72\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}24x-9y=216\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x-9y+7x+9y=216-2\\8x-3y=72\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}31x=214\\3y=8x-72\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{214}{31}\\y=\dfrac{8x-72}{3}=\dfrac{-520}{93}\end{matrix}\right.\)

3) Với a = 3 ta có hpt:
\(\left\{{}\begin{matrix}2x+3y=5\\3x+2y=2\cdot3+1=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+9y=15\\6x+4y=14\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5y=1\\2x+3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{5}\\2x+\dfrac{3}{5}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{5}\\2x=5-\dfrac{3}{5}=\dfrac{22}{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{5}\\x=\dfrac{11}{5}\end{matrix}\right.\)
2: ĐKXĐ: \(\left\{{}\begin{matrix}x\ne2\\y\ne1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\dfrac{2}{x-2}+\dfrac{2}{y-1}=2\\\dfrac{2}{x-2}-\dfrac{3}{y-1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x-2}+\dfrac{2}{y-1}-\dfrac{2}{x-2}+\dfrac{3}{y-1}=2-1\\\dfrac{1}{x-2}+\dfrac{1}{y-1}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5}{y-1}=1\\\dfrac{1}{x-2}=1-\dfrac{1}{y-1}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-1=5\\\dfrac{1}{x-2}=1-\dfrac{1}{5}=\dfrac{4}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y-1=5\\x-2=\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=6\\x=2+\dfrac{5}{4}=\dfrac{8}{4}+\dfrac{5}{4}=\dfrac{13}{4}\end{matrix}\right.\left(nhận\right)\)

a: Để hệ có nghiệm duy nhất thì \(\dfrac{3}{2}\ne\dfrac{a}{1}\)
=>\(a\ne1,5\)
b: Để hệ vô nghiệm thì \(\dfrac{3}{2}=\dfrac{a}{1}\ne\dfrac{5}{b}\)
=>\(\left\{{}\begin{matrix}a=\dfrac{3}{2}\\b\ne\dfrac{10}{3}\end{matrix}\right.\)
c: Để hệ có vô số nghiệm thì \(\dfrac{3}{2}=\dfrac{a}{1}=\dfrac{5}{b}\)
=>\(\left\{{}\begin{matrix}a=1\cdot\dfrac{3}{2}=\dfrac{3}{2}\\b=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\end{matrix}\right.\)

ĐKXĐ: \(x\ne\pm y\)
Phương trình ở dưới thiếu vế phải rồi bạn
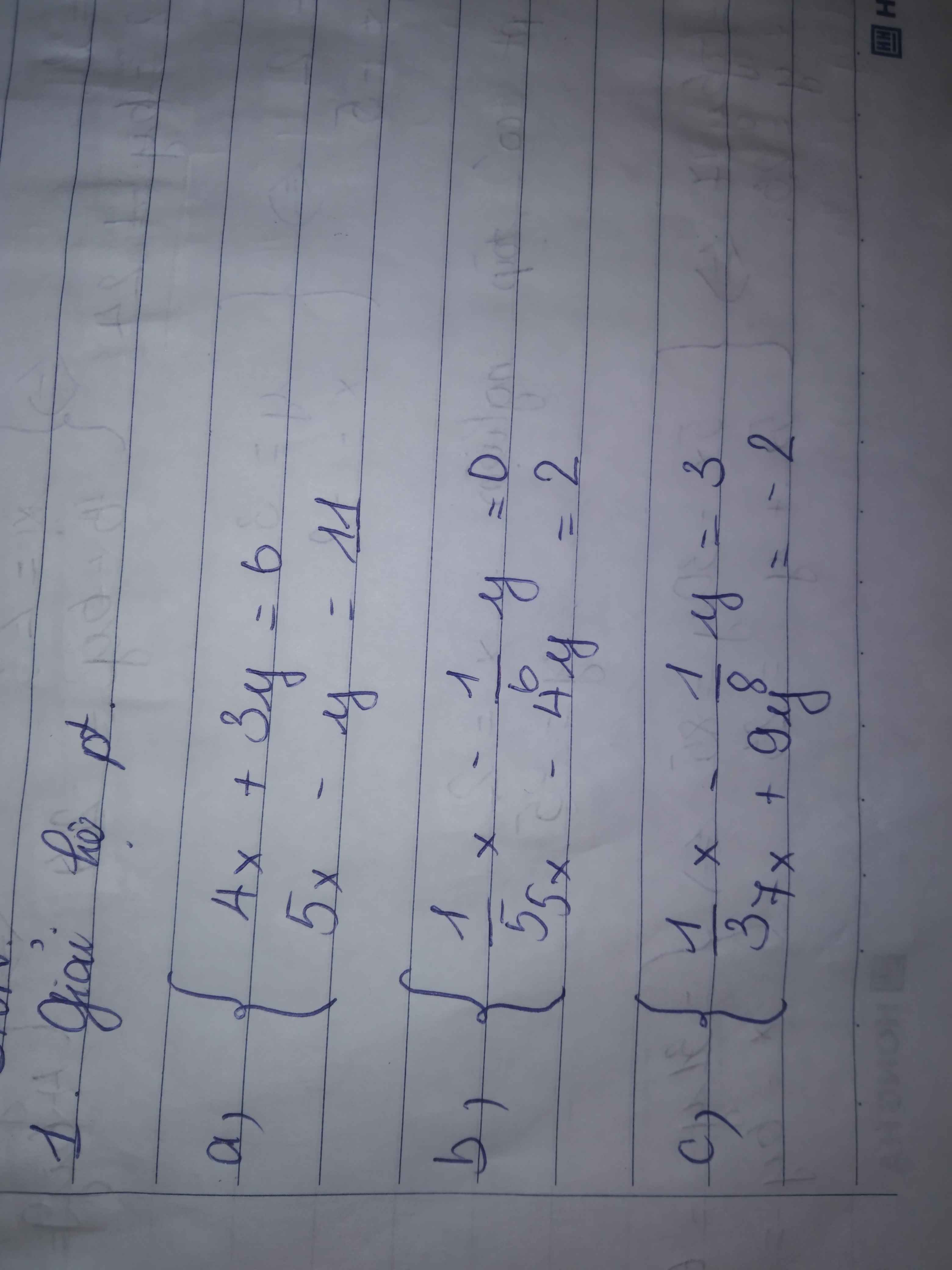
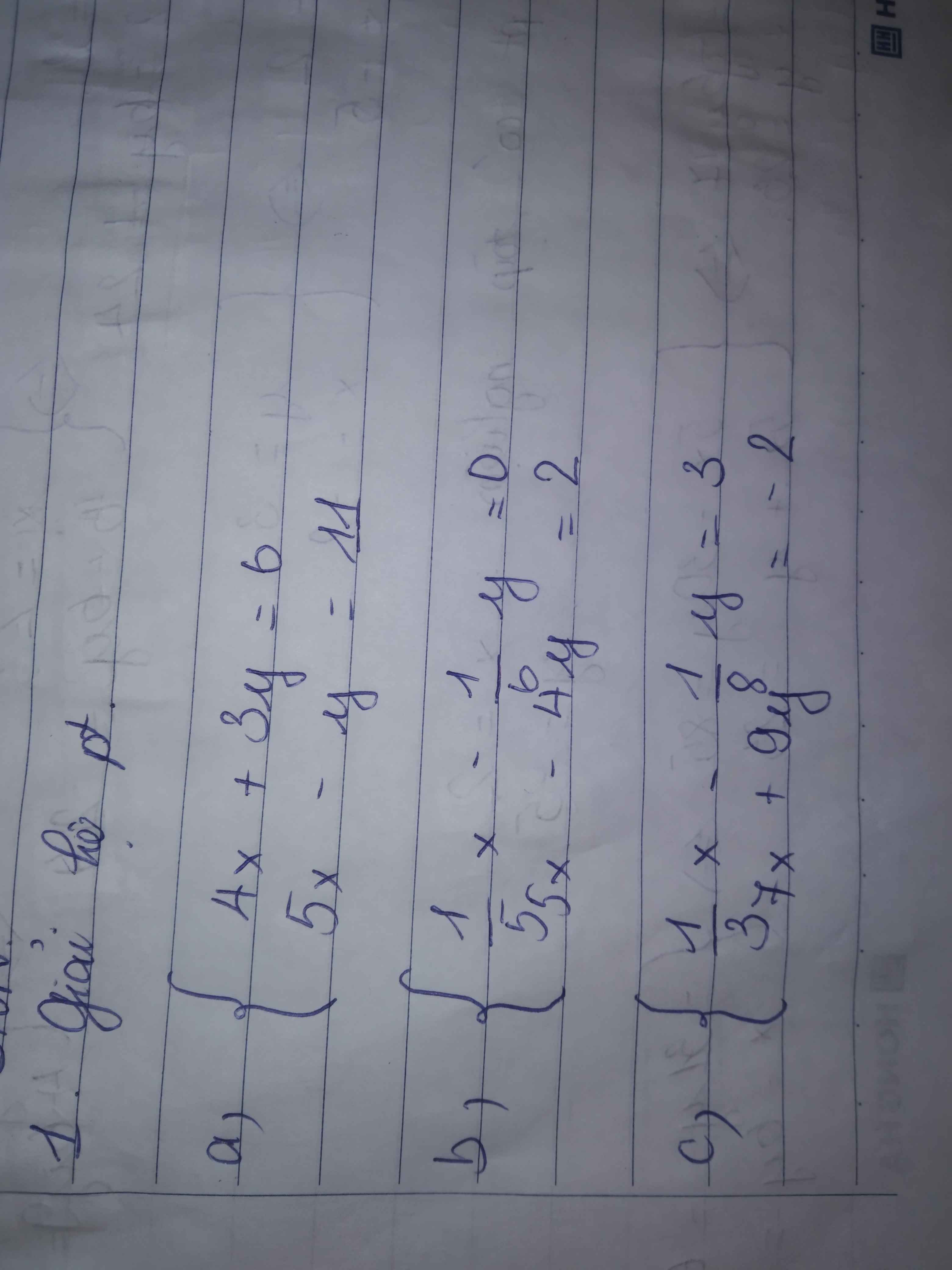
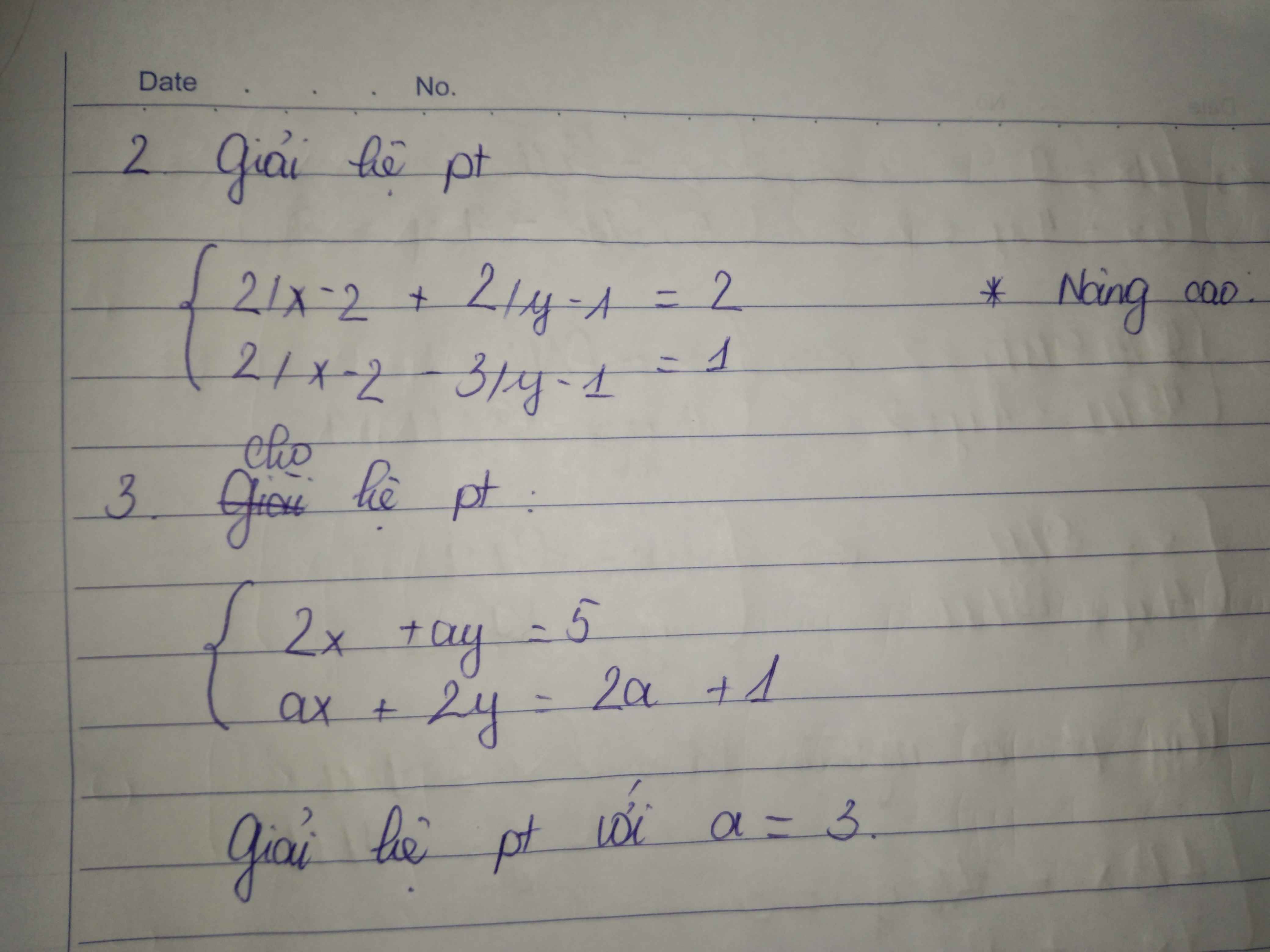
a: \(\left\{{}\begin{matrix}4x+3y=6\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\15x-3y=33\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+3y+15x-3y=6+33\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19x=39\\y=5x-11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{39}{19}\\y=5\cdot\dfrac{39}{19}-11=-\dfrac{14}{19}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{1}{5}x-\dfrac{1}{6}y=0\\5x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=\dfrac{y}{6}\\5x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\5\cdot\dfrac{5}{6}y-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{25}{6}y-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{1}{6}y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\x=\dfrac{5}{6}\cdot12=10\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{1}{3}x-\dfrac{1}{8}y=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}-\dfrac{y}{8}=3\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8x-3y}{24}=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x-3y=72\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}24x-9y=216\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x-9y+7x+9y=216-2\\8x-3y=72\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}31x=214\\3y=8x-72\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{214}{31}\\y=\dfrac{8x-72}{3}=\dfrac{-520}{93}\end{matrix}\right.\)
mọi người giúp e với ạ