Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Olm chào em, đây là dạng toán nâng cao hai tỉ số, cấu trúc thi chuyên, thi học sinh giỏi, thi violympic. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Bước 1: từ hai tỉ số tìm ra tỉ số số cam và số quýt
Bước 2: từ hai tỉ số tìm được ở bước 1 kết hợp với tổng trở thành toán tổng tỉ. Giải toán tổng tỉ thông thường tìm được số cam, số quýt lúc đầu mỗi loại.
Giải:
Số cam còn lại bằng: 1 - \(\dfrac{2}{3}\)= \(\dfrac{1}{3}\) (số cam lúc đầu)
Theo bài ra ta có: \(\dfrac{1}{3}\) số cam lúc đầu = \(\dfrac{1}{4}\) số quýt lúc đầu
Tỉ số số cam lúc đầu và số quýt lúc đầu là: \(\dfrac{1}{4}\): \(\dfrac{1}{3}\) = \(\dfrac{3}{4}\)
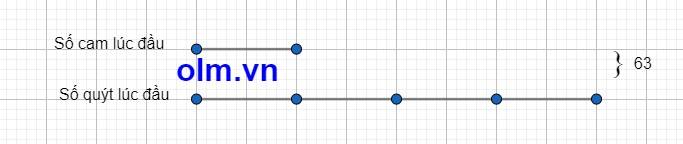
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Số cam lúc đầu là: 63 : (3 + 4) x 3 = 27 (quả)
Số quýt lúc đầu là: 63 - 27 = 36 (quả)
Đáp số: số cam lúc đầu là 27 quả
số quýt lúc đầu là 36 quả

Số sách lớp 6A quyên góp được là:
\(40:\dfrac{2}{3}=60\) (quyển)
Tổng số sách cả 3 lớp quyên góp được là:
\(60.4=240\) (quyển)
Tổng số sách lớp 6B và 6C quyên góp được là:
\(240-60=180\) (quyển)
Số sách lớp 6B quyên góp được là:
\(180.2:3=120\) (quyển)
Số sách lớp 6C quyên góp được là:
\(180-120=60\) (quyển)

Diện tích phần trồng rau là:
\(280\times\dfrac{2}{5}=112\left(m^2\right)\)
Diện tích phần trồng hoa là:
\(280-112=168\left(m^2\right)\)


a.
Số củ cải là:
\(48\times12,5\%=6\) (củ)
Số cà rốt là:
\(\left(48-6\right)\times\dfrac{3}{7}=18\) (củ)
Số khoai tây là:
\(48-\left(6+18\right)=24\) (củ)
b.
Khoai tây chiếm phần trăm so với tổng số rau củ là:
\(\left(\dfrac{24.100}{48}\right)\%=50\%\)

Quãng đường xe đã đi là:
\(125920,5-125454,7=465,8\left(km\right)\)
Số tiền xăng xe đã tiêu thụ là:
\(\dfrac{465,8}{8,5}\times22700=1243960\) (đồng)
Mỗi người bạn của anh Minh phải trả số tiền là:
\(1243960:4=310990\) (đồng)

a: Ta có: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-60^0=30^0\)
b: Sửa đề; BE là phân giác của góc B
Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
BA=BH
Do đó: ΔBAE=ΔBHE
=>\(\widehat{ABE}=\widehat{HBE}\)
=>BE là phân giác của góc ABC
c: Xét ΔBKC có
CA,KH là các đường cao
KH cắt CA tại E
Do đó: E là trực tâm của ΔBKC
=>BE\(\perp\)KC
d: Xét ΔABC vuông tại A có \(cosB=\dfrac{BA}{BC}=\dfrac{1}{2}\)
nên \(\widehat{B}=60^0\)



a: Xét ΔCAD vuông tại A và ΔCHD vuông tại H có
CD chung
\(\widehat{ACD}=\widehat{HCD}\)
Do đó: ΔCAD=ΔCHD
=>CA=CH
b: Ta có: ΔCAD=ΔCHD
=>DA=DH
=>D nằm trên đường trung trực của AH(1)
Ta có: CA=CH
=>C nằm trên đường trung trực của AH(2)
Từ (1),(2) suy ra CD là đường trung trực của AH
=>CD\(\perp\)AH tại I và I là trung điểm của AH
c: GI=1/2GB
=>BG=2GI
=>\(\dfrac{BG}{BI}=\dfrac{2}{3}\)
Xét ΔHAB có
BI là đường trung tuyến
\(BG=\dfrac{2}{3}BI\)
Do đó: G là trọng tâm của ΔHAB
Xét ΔHAB có
G là trọng tâm
K là trung điểm của AB
DO đó: H,K,G thẳng hàng