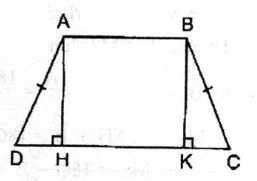
Hình thang cân ABCD có AB // CD, AB < CD. Kẻ các đường cao AH, BK. |
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có :
\(-b^3+6b^2-13b+8=-b^3+b^2+5b^2-5b-8b+8\)
\(=-\left(b-1\right)\left(b^2-5b+8\right)\)

a) 9x2y2 - 6xy2 + y2
= y2(9x2 - 6x + 1)
= y2(3x - 1)2
b) x3 + 27 - 3x(x + 3)
= (x + 3)(x2 - 3x + 9) - 3x(x + 3)
= (x + 3)(x2 - 6x + 9)
= (x + 3)(x - 3)2
c) x2 - 2x - 4y2 - 4y
= x2 - 2x + 1 - 4y2 - 4y - 1
= (x - 1)2 - (2y + 1)2
= (x + 2y)(x - 2y - 2)
d) a4 - 2a2b2 + b4
= (a2 - b2)2
= [(a - b)(a + b)]2
9x2y2 - 6xy2 + y2 = ( 3xy - y )2 = y2 ( 3x - 1 )2
x3 + 27 - 3x(x + 3 ) = ( x + 3 ) ( x2 - 3x + 9) - 3x ( x + 3 )
= ( x + 3 ) ( x2 - 6x + 9 )
= ( x + 3 ) ( x - 3 ) 2
x2 - 2x - 4y2 - 4y = ( x - 2y ) ( x + 2y ) - 2 ( x + 2y ) = ( x + 2y ) ( x - 2y - 2 )
a4 - 2a2b2 + b4 = ( a2 - b2 )2 = ( a - b )2 ( a + b )2

x3 + 2x2 - x - 2 = 0
<=> x2(x + 2) - (x + 2) = 0
<=> (x2 - 1)(x + 2) = 0
<=> (x - 1)(x + 1)(x + 2) = 0
<=> x - 1 = 0 hoặc x + 1 = 0 hoặc x + 2 = 0
<=> x = 1 hoặc x = -1 hoặc x = -2
Vậy \(x\in\left\{1;-1;-2\right\}\)là nghiệm phương trình
đề bài
---> \(x^3-x^2+3x^2-3x+2x-2=0\)
---> \(x^2\left(x-1\right)+3x\left(x-1\right)+2\left(x-1\right)=0\)
---> \(\left(x-1\right)\left(x^2+3x+2\right)=0\)
---> \(\left(x-1\right)\left(x+1\right)\left(x+2\right)=0\)
---> \(\hept{\begin{cases}x=1\\x=-1\\x=2\end{cases}}\)
bạn thay dấu ngoặc nhọn bằng dấu ngoặc vuông
xin tiick

Bài giải
( Hình tự vẽ, tự ghi GT, KL)
a) Ta có: PQGH hình bình hành ( GT)
=> HO=OQ=PO=OG ( Đ/lý)
Ta có : M trđ HO; N trđ OQ ( GT)
=> HM=MO=NO=QN
=> O trđ MN (1)
Ta có :PO=PG( cmt)
=> O trđ PG (2)
Từ (1), (2) => PMGN hình bình hành ( Đ/lý)
b, Vì PMGN hình bình hành (cmt)
Nên NG // PM
=> FG // PE
Mà PF // EG ( vì PQ//HG, F thuộc PQ và E thuộc HG )
=> PFGE là hình bình hành
Mà O là trung điểm của PG
=> O là trung điểm của EF
Vậy E đối xứng với F qua O (Đpcm)
c, Ta có : PE//FG (cmt)
Mà M thuộc PE; N thuộc FG => ME // NG
Xét tam giác HNG, ta có:ME//NG (cmt)
=> ME đường trug bình tam giác HNG
=> M trđ HN; E trđ HG ( Đ/lý)
=> HE=\(\frac{1}{2}\)HG (Đpcm)
Chúc bạn học tốt!
Nếu thấy hay hãy !
Bài giải
( Hình tự vẽ, tự ghi GT, KL)
a) Ta có: PQGH hình bình hành ( GT)
=> HO=OQ=PO=OG ( Đ/lý)
Ta có : M trđ HO; N trđ OQ ( GT)
=> HM=MO=NO=QN
=> O trđ MN (1)
Ta có :PO=PG( cmt)
=> O trđ PG (2)
Từ (1), (2) => PMGN hình bình hành ( Đ/lý)
b, Vì PMGN hình bình hành (cmt)
Nên NG // PM
=> FG // PE
Mà PF // EG ( vì PQ//HG, F thuộc PQ và E thuộc HG )
=> PFGE là hình bình hành
Mà O là trung điểm của PG
=> O là trung điểm của EF
Vậy E đối xứng với F qua O (Đpcm)
c, Ta có : PE//FG (cmt)
Mà M thuộc PE; N thuộc FG => ME // NG
Xét tam giác HNG, ta có:ME//NG (cmt)
=> ME đường trug bình tam giác HNG
=> M trđ HN; E trđ HG ( Đ/lý)
=> HE=\(\frac{1}{2}\)HG (Đpcm)
Chúc bạn học tốt!
Nếu thấy hay hãy !



Ta có A = \(\frac{6x-2}{3x^2+1}=\frac{3x^2+1-3x^2+6x-3}{3x^2+1}=1-\frac{3\left(x-1\right)^2}{3x^2+1}\le1\)
=> Max A = 1
Dấu "=" xảy ra <=> x - 1 = 0
<=> x = 1
Vậy Max A = 1 <=> x = 1
Lại có A = \(\frac{6x-2}{3x^2+1}=\frac{-9x^2-3+9x^2+6x+1}{3x^2+1}=-3+\frac{\left(3x+1\right)^2}{3x+1}\ge-3\)
Dấu "=" xảy ra <=> 3x + 1 = 0
<=> x = -1/3
Vậy Min A = -3 <=> x = -1/3

Ta có :
\(\left(x^2-3x-2\right):\left(x-2\right)=\frac{\left(x-1\right)\left(x-2\right)}{x-2}=x-1\)

Tranh đây ...