Tìm ĐKXĐ của \(P=\frac{2\sqrt{x-1}}{1-\sqrt{4x+3-4\sqrt{3x}}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi chiều dài hình chữ nhật ban đầu là \(x\left(m\right),x>0\).
Chiều rộng hình chữ nhật ban đầu là: \(\frac{240}{x}\left(m\right)\).
Chiều rộng mới là: \(\frac{240}{x}+3\left(m\right)\).
Chiều dài mới là: \(x-4\left(m\right)\).
Ta có phương trình: \(\left(x-4\right)\left(\frac{240}{x}+3\right)=240\)
\(\Rightarrow\left(x-4\right)\left(240+3x\right)=240x\)
\(\Leftrightarrow x^2+76x-320=80x\)
\(\Leftrightarrow x^2-4x-320=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=20\left(tm\right)\\x=-16\left(l\right)\end{cases}}\)
Chu vi hình chữ nhật ban đầu là: \(2\left(20+\frac{240}{20}\right)=64\left(m\right)\).

Ơ chị j ơi sem lại đề bài ik ạ
\(\left(\frac{1-x\sqrt{x}}{\left(1-1\right)}+\sqrt{x}\right)\)Cái phần 1-1 iem cho trong ngoặc ấy thì nó bằng 0 => vô lý với phân số làm sao chia 0 đc :))

a, Để pt có 2 nghiệm phân biệt khi \(\Delta>0\)
\(=16-4\left(m+1\right)=12-4m>0\Leftrightarrow m< 3\)
b, Thay m = 1 vào pt trên ta được :
\(x^2-4x+2=0\Leftrightarrow x^2-4x+4-2=0\)
\(\Leftrightarrow\left(x-2\right)^2-2=0\Leftrightarrow\left(x-2\pm\sqrt{2}\right)=0\Leftrightarrow x=2\pm\sqrt{2}\)
c, Theo Vi et ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=4\\x_1x_2=\frac{c}{a}=m+1\end{cases}}\)
\(\left(1\right)\Rightarrow x_2=4-x_1=4+1=5\)
Thay vào (2) ta được : \(-5=m+1\Leftrightarrow m=-6\)

\(\left(\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\right)^2\)
\(=4+\sqrt{7}+4-\sqrt{7}-2\sqrt{\left(4+\sqrt{7}\right)\left(4-\sqrt{7}\right)}\)
\(=8-2\sqrt{16-7}\)
\(=8-6=2\)

Ta xét \(6\)nhóm có chữ số tận cùng là \(0,1-9,2-8,3-7,4-6,5\).
Theo nguyên lí Dirichlet có ít nhất \(1\)nhóm có ít nhất \(2\)phần tử. Ta chọn \(2\)số thuộc nhóm đó, dễ thấy ta có đpcm.

B1 : giải PT (m tham số ) bằng cách tính denta > 0
B2 : áp dụng hệ thức VI-ÉT .. X1 + X2 = -b/a
.. X1X2 = c/a
B3: thay x1 + x2 = -b/a vào pt (2)
thay x1x2 = c/a vào pt (2)
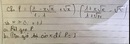
ĐKXĐ : \(1-\sqrt{4x+3-4\sqrt{3x}}\ne0\)
\(\Leftrightarrow\sqrt{4x+3-4\sqrt{3x}}\ne1\)
\(\Leftrightarrow\left|4x+3-4\sqrt{3x}\right|\ne1\)
TH1 : \(4x+3-4\sqrt{3x}\ne1\Leftrightarrow\sqrt{3x}\ne\frac{1+2x}{2}\)
\(\Leftrightarrow3x\ne\frac{1+4x+4x^2}{4}\Leftrightarrow4x^2-8x+1\ne0\)
\(\Leftrightarrow x\ne1\pm\frac{\sqrt{3}}{2}\)
TH2 : \(4x+3-4\sqrt{3x}\ne-1\Leftrightarrow\sqrt{3x}\ne x+1\)
\(\Leftrightarrow3x\ne x^2+2x+1\Leftrightarrow x^2-x+1\ne0\)* luôn đúng *