3 mình giải cho bạn rồi

4                  giải

a)s

b)đ

1                    giai

có 9 góc nhọn,6 góc vuông,6 góc tù

Bài 8:

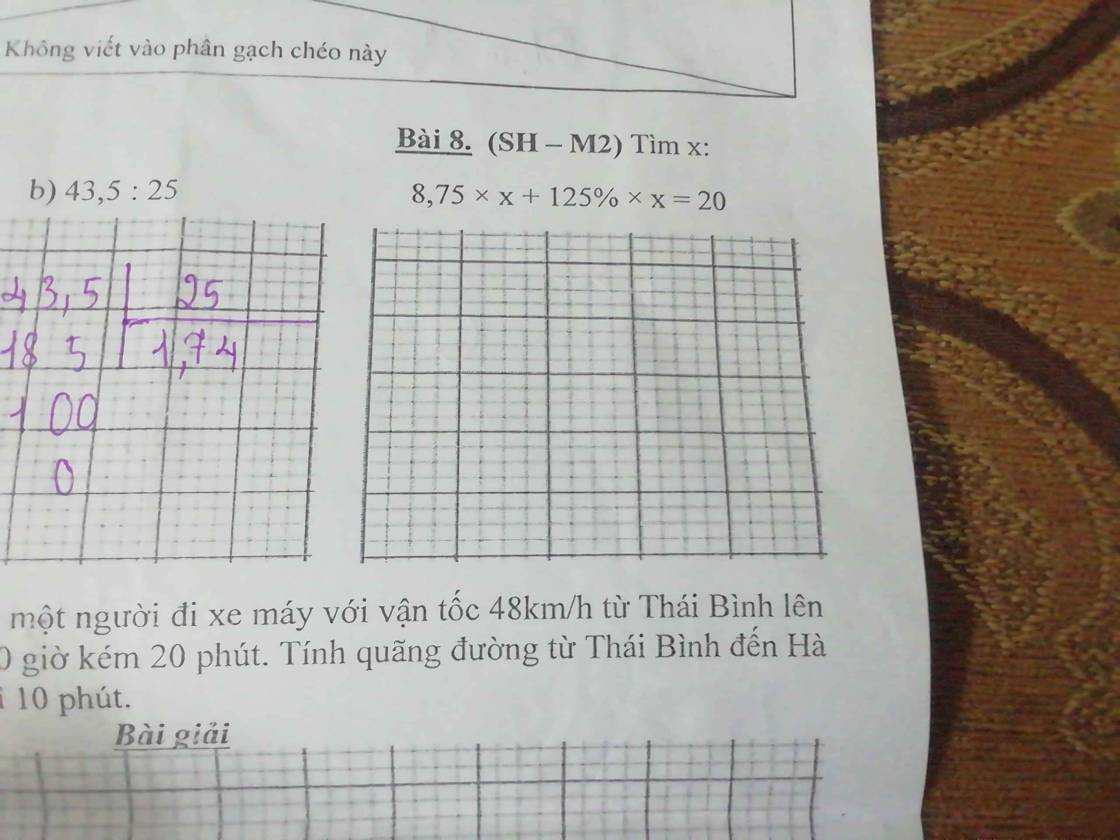
\(8,75\times X+125\%\times X=20\)

=>\(8,75\times X+1,25\times X=20\)

=>\(X\times\left(8,75+1,25\right)=20\)

=>\(X\times10=20\)

=>X=20:10=2

ĐKXĐ: \(x\ge2\)

\(\sqrt{4x-8}-\sqrt{x-2}=2\)

\(\Leftrightarrow\sqrt{4\left(x-2\right)}-\sqrt{x-2}=2\)

\(\Leftrightarrow2\sqrt{x-2}-\sqrt{x-2}=2\)

\(\Leftrightarrow\sqrt{x-2}=2\)

\(\Leftrightarrow x-2=4\)

\(\Leftrightarrow x=6\) (thỏa mãn)

484

Tim n nguyên để A = \(\dfrac{n-1}{n+2}\) thỏa mãn điều gì em ơi?

Hình như là để A có giá trị nguyên á cô.

\(E\left(x\right)=2x+1=0\)

\(\Rightarrow2x=-1\)

\(\Rightarrow x=-\dfrac{1}{2}\)

Vậy \(x=-\dfrac{1}{2}\) là nghiệm của đa thức

\(E\left(x\right)=0\Rightarrow2x+1=0\)

\(\Rightarrow2x=-1\)

\(\Rightarrow x=\dfrac{-1}{2}\)

Vậy...

a: Xét ΔBAH và ΔBDH có

BA=BD

AH=DH

BH chung

Do đó: ΔBAH=ΔBDH

b: ΔBAH=ΔBDH

=>\(\widehat{ABH}=\widehat{DBH}\)

Xét ΔBAE và ΔBDE có

BA=BD

\(\widehat{ABE}=\widehat{DBE}\)

BE chung

Do đó: ΔBAE=ΔBDE

=>EA=ED

=>ΔEAD cân tại E

c: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}=30^0\)

Xét ΔEDC vuông tại D có \(sinECD=\dfrac{ED}{EC}\)

=>\(\dfrac{EA}{EC}=sin30=\dfrac{1}{2}\)

=>EC=2AE

vẽ hình nx nhé bạn

\(\left(x-3\right)\left(2x+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\2x+4=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)

\(\left(x-3\right)\)\(\left(2x-4\right)\)\(=\) \(0\)

\(\Rightarrow\) \(\left(x-3\right)\)\(=\) \(0\)  hoặc \(\left(2x-4\right)\)\(=\) \(0\)

\(TH1:\) \(\left(x-3\right)\)\(=\) \(0\)

            \(x\)         \(=\) \(0\) \(+\) \(3\)

            \(x\)         \(=\) \(3\)

\(TH2:\) \(\left(2x+4\right)\)\(=\) \(0\)

            \(2x\)        \(=\) \(0\) \(-\) \(4\)

            \(2x\)        \(=\) \(-4\)

              \(x\)        \(=\)  \(-4\) \(:\) \(2\)

              \(x\)        \(=\) \(-2\)

Vậy \(x\) \(\in\) { \(3\) \(;\) \(-2\) }

Với mọi a;b;c ta có

\(\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\)

\(\Leftrightarrow a^2+b^2+c^2\ge2\left(a+b+c\right)-3\) (1)

Lại có:

\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)

\(\Leftrightarrow2a^2+2b^2+2c^2\ge2ab+2bc+2ca\)

\(\Leftrightarrow6a^2+6b^2+6c^2\ge6ab+6bc+6ca\) (2)

Cộng vế (1) và (2):

\(7\left(a^2+b^2+c^2\right)\ge2\left(a+b+c+3ab+3bc+3ca\right)-3=2.12-3=21\)

\(\Rightarrow a^2+b^2+c^2\ge3\)

Dấu "=" xảy ra khi \(a=b=c=1\)