tìm đa thức M sao cho tổng của M với đa thức x^2 -2xy+ y^2 -2xz+z^2 ko chứa biến x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,A=x^2+y^2+2x-6y-2\\ =\left(x^2+2x+1\right)+\left(y^2-6y+9\right)-12\\ =\left(x+1\right)^2+\left(y-3\right)^2-12\)
Ta có:
`(x+1)^2>=0` với mọi x
`(y-3)^2>=0` với mọi y
`=>A=(x+1)^2+(y-3)^2-12>=-12` với mọi x,y
Dấu "=" xảy ra: `x+1=0` và `y-3=0`
`<=>x=-1` và `y=3`
\(b,B=5x^2+y^2+z^2+4xy+2xz\\ =\left(4x^2+4xy+y^2\right)+\left(x^2+2xz+z^2\right)\\ =\left(2x+y\right)^2+\left(x+z\right)^2\)
Ta có:
`(2x+y)^2>=0` với mọi x,y
`(x+z)^2>=0` với mọi x,z
`=>B=(2x+y)^2+(x+z)^2>=0`
Dấu "=" xảy ra: `2x+y=0` và `x+z=0`
`<=>2x=-y=-2z`
\(c,C=2x^2+y^2+2xy-8x+2024\\ =\left(x^2+2xy+y^2\right)+\left(x^2-8x+16\right)+2008\\ =\left(x+y\right)^2+\left(x-4\right)^2+2008\)
Ta có:
`(x+y)^2>=0` với mọi x,y
`(x-4)^2>=0` với mọi x
`=>C=(x+y)^2+(x-4)^2+2008>=2008`
Dấu "=" xảy ra:
`x+y=0` và `x-4=0`
`<=>x=4` và `y=-4`
\(d,D=x^2-2xy+3y^2-2x+1997\\ =\left(x^2+y^2+1-2xy-2x+2y\right)+\left(2y^2-2y+\dfrac{1}{2}\right)+\dfrac{3991}{2}\\ =\left(-x+y+1\right)^2+2\left(y^2-y+\dfrac{1}{4}\right)+\dfrac{3991}{2}\\ =\left(-x+y+1\right)^2+2\left(y-\dfrac{1}{2}\right)^2+\dfrac{3991}{2}\)
Ta có:
`(-x+y+1)^2>=0` với mọi x,y
`2(y-1/2)^2>=0` với mọi y
`=>D=(-x+y+1)^2+2(y-1/2)^2+3991/2>=3991/2`
Dấu "=" xảy ra: `-x+y+1=0` và `y-1/2=0`
`<=>y=1/2` và `x=3/2`

\(5,8a^3\left(a-b\right)-27\left(a-b\right)\\ =\left(a-b\right)\left(8a^3-27\right)\\ =\left(a-b\right)\left(2a-3\right)\left(4a^2+6a+9\right)\\ 6,27\left(a+b\right)-a^3\left(a+b\right)\\ =\left(a+b\right)\left(27-a^3\right)\\ =\left(a+b\right)\left(3-a\right)\left(9+3a+a^2\right)\\ 7,8a^3\left(2a-3b\right)+27\left(2a-3b\right)\\ =\left(2a-3b\right)\left(8a^3+27\right)\\ =\left(2a-3b\right)\left(2a+3\right)\left(4a^2-6a+9\right)\)

That's the easiest question to answer
This textbook is easy to understand

Xét tứ giác MNPQ ta có:
\(\widehat{M}+\widehat{N}+\widehat{P}+\widehat{Q}=360^o\) (tổng các góc trong tam giác)\
\(\widehat{M}:\widehat{N}:\widehat{P}:\widehat{Q}=1:2:3:4\\ =>\dfrac{\widehat{M}}{1}=\dfrac{\widehat{N}}{2}=\dfrac{\widehat{P}}{3}=\dfrac{\widehat{Q}}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{\widehat{M}}{1}=\dfrac{\widehat{N}}{2}=\dfrac{\widehat{P}}{3}=\dfrac{\widehat{Q}}{4}=\dfrac{\widehat{M}+\widehat{N}+\widehat{Q}+\widehat{Q}}{1+2+3+4}=\dfrac{360^o}{10}=36^o\\ =>\widehat{M}=36^o\\ =>\dfrac{\widehat{N}}{2}=36^o=>\widehat{N}=72^o\\ =>\dfrac{\widehat{P}}{3}=36^o=>\widehat{P}=108^o\\ =>\dfrac{\widehat{Q}}{4}=36^o=>\widehat{Q}=144^o\)
Vì: \(\widehat{M}+\widehat{Q}=36^o+144^o=180^o\) => MN//PQ => MNPQ là hình thang

\(IF\) \(you\) \(are\) \(lazy\) \(to\) \(learn\) \(lessons\),\(you\) \(will\) \(always\) \(get\) \(bad\) \(marks\)

\(n_{Al}=\dfrac{27.1000}{27}=1000\left(kmol\right)\)
\(Al_2O_3\xrightarrow[criolic]{đpnc}2Al+3O_2\)
500<------1000 (kmol)
\(m_{Al_2O_3\left(lý.thuyết\right)}=500.102=51000\left(kg\right)\)
H% = 85% => \(m_{Al_2O_3\left(thực.tế\right)}=\dfrac{51000.100\%}{85\%}=60000\left(kg\right)=60\left(tấn\right)\)
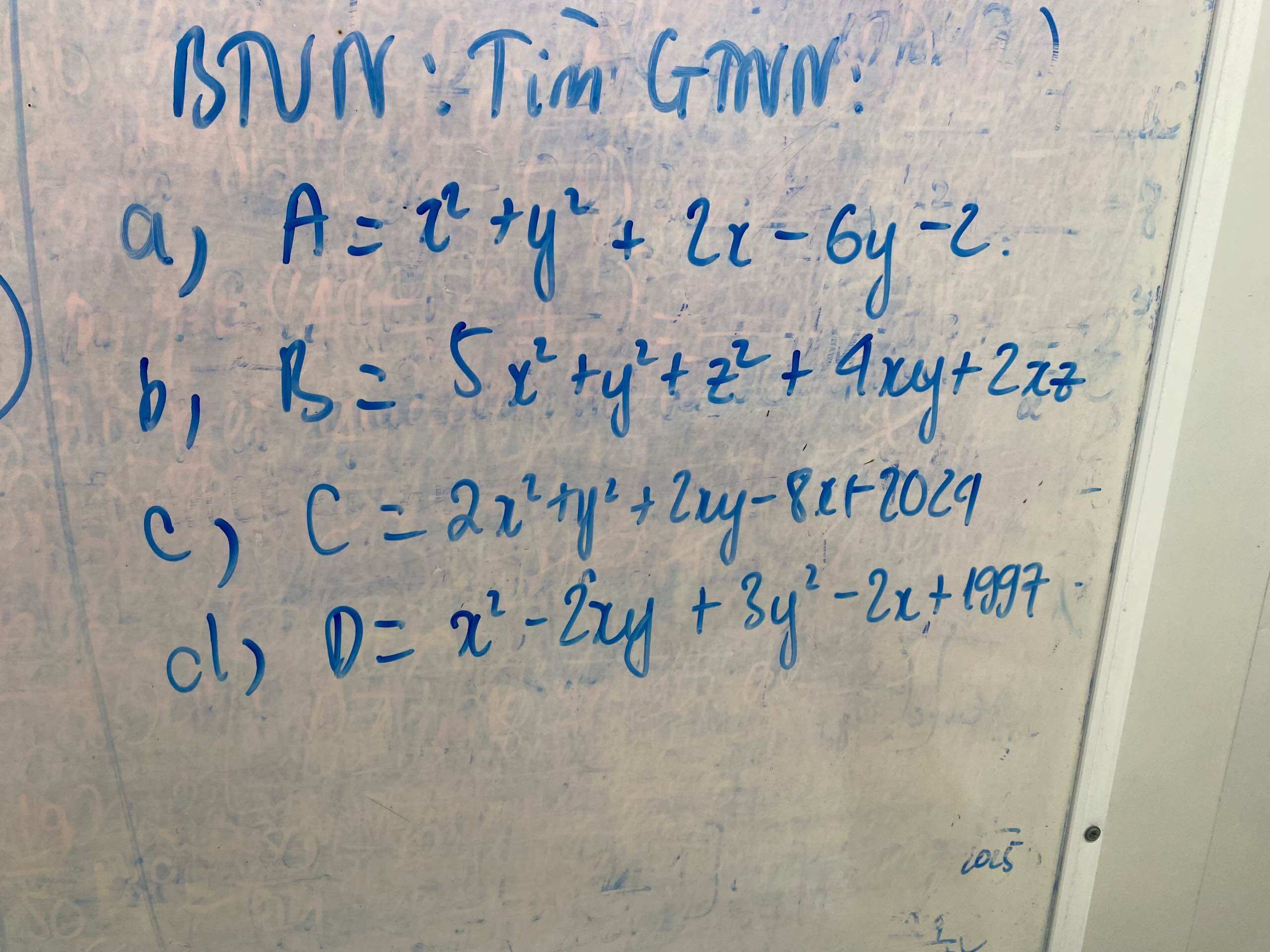
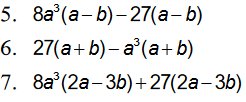 Giúp mik với ạ
Giúp mik với ạ

Để tổng của M với đa thức \(x^2-2xy+y^2-2xz+z^2\) không chứa biến x thì \(M+x^2-2xy+y^2-2xz+z^2=y^2+z^2\)
=>\(M+x^2-2xy-2xz=0\)
=>\(M=-x^2+2xy+2xz\)
Cho tam giác ABC vuông tại A,biết AB=3cm,AC=4cm,tính BC