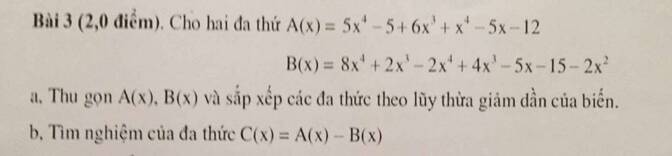
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
Vế trái luôn không âm (tính chất trị tuyệt đối)
$\Rightarrow -11x\geq 0$
$\Rightarrow x\leq 0$
Do đó: $x-\frac{1}{3}, x-\frac{1}{15},..., x-\frac{1}{399}<0$
PT trở thành:
$\frac{1}{3}-x+\frac{1}{15}-x+...+\frac{1}{399}-x=-11x$
$(\frac{1}{3}+\frac{1}{15}+...+\frac{1}{399})-10x=-11x$
$\frac{1}{1.3}+\frac{1}{3.5}+...+\frac{1}{19.21}=-x$
$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+..+\frac{1}{19}-\frac{1}{21})=-x$
$\frac{1}{2}(1-\frac{1}{21})=-x$
$\frac{10}{21}=-x$
$\Rightarrow x=\frac{-10}{21}$
Lời giải:
Vế trái luôn không âm (tính chất trị tuyệt đối)
$\Rightarrow -11x\geq 0$
$\Rightarrow x\leq 0$
Do đó: $x-\frac{1}{3}, x-\frac{1}{15},..., x-\frac{1}{399}<0$
PT trở thành:
$\frac{1}{3}-x+\frac{1}{15}-x+...+\frac{1}{399}-x=-11x$
$(\frac{1}{3}+\frac{1}{15}+...+\frac{1}{399})-10x=-11x$
$\frac{1}{1.3}+\frac{1}{3.5}+...+\frac{1}{19.21}=-x$
$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+..+\frac{1}{19}-\frac{1}{21})=-x$
$\frac{1}{2}(1-\frac{1}{21})=-x$
$\frac{10}{21}=-x$
$\Rightarrow x=\frac{-10}{21}$

Vì \(\left(x-3\right)^2\ge0\Rightarrow\left(x-3\right)^2+1>0\)
Vậy pt vô nghiệm

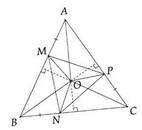
a, Vì \(\Delta ABC\) đều và \(O\) là giao điểm 3 đường trung trực nên \(AO\) là tia phân giác của \(\widehat{A}\)
\(\Rightarrow\widehat{MAO}=\dfrac{\widehat{BAC}}{2}=30^o\)
b, Tương tự a, \(\widehat{OCB}=30^o\)
Chứng minh được: \(\Delta MAO=\Delta OPC\left(c.g.c\right)\)
Ta có: \(\Delta MAO=\Delta OPC\Rightarrow OM=OP\left(1\right)\)
c, Tương tự b
\(\Delta MAO=\Delta NBO\left(c.g.c\right)\)
\(\Rightarrow ON=OM\left(2\right)\)
Từ (1) và (2) suy ra O là giao điểm
3 đương trung trực của tam giác MNP

(3x - 5) - (x - 1) = (x + 6) - (x - 3)
3x - 5 - x + 1 = x + 6 - x + 3
3x - x - x + x = 5 - 1 + 6 + 3
2x = 13
x = 13/2

\(-2x^2+5x=0\\ \Rightarrow x\left(5-2x\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\5-2x=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\2x=5\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{5}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{0;\dfrac{5}{2}\right\}\)
a,
\(A\left(x\right)=5x^4-5+6x^3+x^4-5x-12\)
\(=\left(5x^4+x^4\right)+6x^3-5x+\left(-5-12\right)\)
\(=6x^4+6x^3-5x-17\)
\(B\left(x\right)=8x^4+2x^3-2x^4+4x^3-5x-14-2x^2\)
\(=\left(8x^4-2x^4\right)+\left(2x^3+4x^3\right)-2x^2-5x-15\)
\(=6x^4+6x^3-2x^2-5x-15\)
b,
\(C\left(x\right)=A\left(x\right)-B\left(x\right)=\left(6x^4+6x^3-5x-17\right)-\left(6x^4+6x^3-2x^2-5x-15\right)\)
\(=\left(6x^4-6x^4\right)+\left(6x^3-6x^3\right)+2x^2+\left(-5x+5x\right)+\left(-17+15\right)\)
\(=2x^2-2\)
Để cho đa thức \(C\left(x\right)\) có nghiệm thì \(2x^2-2=0\)
\(\Rightarrow2x^2=2\)
\(\Rightarrow x^2=1\)
\(\Rightarrow x=\pm1\)