Một tổ có 4 xe chở hàng. Xe I chở 3,15 tấn hàng. Xe II chở ít hơn xe I là 0,7 tấn và chở ít hơn xe III là 1,05 tấn. Xe IV chở kém mức trung bình của cả tổ là 0,1 tấn hàng. Hỏi xe IV chở mấy tấn hàng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta lấy đầy bình 9l đổ vào bình 4l số nước còn lại là 5l để riêng
lấy đầy bình 9 l đổ vào bình 4l 2 lần rồi đổ đi.Còn lại 1l để chung với bình 5l.
Ta có 6l cần lấy

\(f\left(x\right)⋮g\left(x\right)\)
=>\(-2x^3-7x^2-5x+5⋮x+2\)
=>\(-2x^3-4x^2-3x^2-6x+x+2+3⋮x+2\)
=>\(3⋮x+2\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)

a: VT=\(\left(a+1\right)\left(a^2-a+1\right)\)
\(=a^3-a^2+a+a^2-a+1\)
\(=a^3+1\)=VP
b: \(VT=\left(a+1\right)\left(a^3-a^2+a-1\right)\)
\(=a^4-a^3+a^2-a+a^3-a^2+a-1\)
\(=a^4-1=VP\)

Tỉ số giữa 30 trang cuối và số trang sách còn lại sau ngày thứ hai là:
\(1-\dfrac{3}{4}=\dfrac{1}{4}\)
Số trang sách còn lại sau ngày 2 là: \(30:\dfrac{1}{4}=120\left(trang\right)\)
2/5 số trang còn lại sau ngày 1 là:
120+20=140(trang)
Số trang sách còn lại sau ngày 1 là:
\(140:\dfrac{2}{5}=350\left(trang\right)\)
2/5 số trang ban đầu là 350+24=374(trang)
Số trang ban đầu là \(374:\dfrac{2}{5}=374\times2,5=935\left(trang\right)\)
Giải:
30 trang ứng với phân số là: 1 - \(\dfrac{3}{4}\) = \(\dfrac{1}{4}\)(số trang còn lại sau ngày thứ hai)
Số trang còn lại sau ngày thứ hai là: 30 : \(\dfrac{1}{4}\) = 120 (trang)
Nếu ngày thứ hai chỉ đọc \(\dfrac{3}{5}\) số trang mà không đọc thêm 20 trang thì còn lại: 120 + 20 = 140 (trang)
140 trang ứng với phân số là:1 - \(\dfrac{3}{5}\) = \(\dfrac{2}{5}\)(số trang còn lại sau ngày thứ nhất)
Số trang còn lại sau ngày thứ nhất là: 140 : \(\dfrac{2}{5}\) = 350 (trang)
Nếu ngày thứ nhất chỉ đọc \(\dfrac{3}{5}\)số trang và không đọc thêm 24 trang thì còn lại: 350 + 24 = 374 (trang)
374 trang ứng với: 1 - \(\dfrac{3}{5}\) = \(\dfrac{2}{5}\) (số trang)
Quyển sách bạn Nam đọc dày số trang là: 374: \(\dfrac{2}{5}\) = 935 (trang)
Đáp số: 935 trang.

Số tiền vốn mua bò là:
\(18000000\times\dfrac{100}{120}=15000000\left(đồng\right)\)
Số tiền vốn mua dê là:
\(8000000:\dfrac{1-20\%}{1}=10000000\left(đồng\right)\)
Tổng số tiền vốn là:
15000000+10000000=25000000(đồng)
Tỉ số giữa số tiền bán được và số tiền vốn là:
\(\dfrac{18000000+8000000}{25000000}=\dfrac{26}{25}=104\%=1+4\%\text{ }\)
=>anh nông lời được 4%

Tỉ số giữa số gạo nếp ban đầu và tổng số gạo là \(\dfrac{75}{75+100}=\dfrac{3}{7}\)
Tỉ số giữa số gạo nếp lúc sau và tổng số gạo là:
\(\dfrac{57}{57+100}=\dfrac{57}{157}\)
\(\dfrac{57}{157}-\dfrac{3}{7}=\dfrac{-72}{1099}\)
\(-\dfrac{72}{1099}\) tổng số gạo ban đầu là:
\(-36+\dfrac{57}{157}\times36=-\dfrac{3600}{157}\left(kg\right)\)
Tổng số gạo ban đầu là \(\dfrac{3600}{157}:\dfrac{72}{1099}=350\left(kg\right)\)
Số gạo nếp ban đầu là \(350\times\dfrac{3}{7}=150\left(kg\right)\)
Số gạo tẻ ban đầu là 350-150=200(kg)
Gọi số gạo tẻ là x, thì số gạo nếp bằng là 0,75x
Sau khi bán được 36kg gạo nếp thì số gạo nếp còn lại là: 0,75x-36
Tỷ số giữa gạo nếp và số gạo tẻ lúc này là: (0,75x-36) = 0,57x
0,18x = 36 suy ra x = 200kg
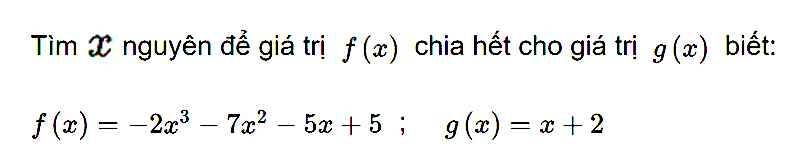
Đây là toán nâng cao chuyên đề trung bình cộng, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các me giải chi tiết dạng này như sau:
Giải:
Xe II chở được số hàng là: 3,15 - 0,7 = 2,45 (tấn)
Xe III chở được số hàng là: 3,15 + 1,05 = 4,2 (tấn)
Tổng số hàng xe I; xe II; xe III chở được là:
3,15 + 2,45 + 4,2 = 9,8 (tấn)
Coi trung bình cộng của cả bốn xe chở được là một phần ta có sơ đồ:
Theo sơ đồ ta có:
Trung bình cộng của bốn xe chở được là:
(9,8 - 0,1) : 3 = \(\dfrac{97}{30}\) (tấn)
Xe IV chở được số tấn hàng là:
\(\dfrac{97}{30}\) - 0,1 = \(\dfrac{47}{15}\) (tấn)
Đáp số: \(\dfrac{47}{15}\) tấn.