a: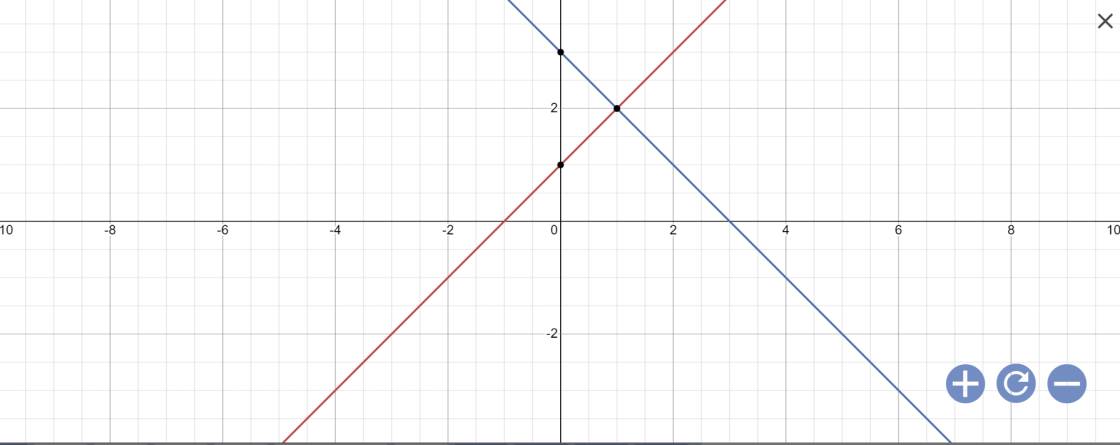

b: tọa độ C là:

\(\left\{{}\begin{matrix}x+1=-x+3\\y=x+1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x=2\\y=x+1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=1\\y=1+1=2\end{matrix}\right.\)

Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\x+1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)

Tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)

Vậy: A(-1;0); B(3;0); C(1;2)

c: A(-1;0); B(3;0); C(1;2)

\(AB=\sqrt{\left(3+1\right)^2+\left(0-0\right)^2}=4\)

\(AC=\sqrt{\left(1+1\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)

\(BC=\sqrt{\left(1-3\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)

Chu vi tam giác ABC là:

\(P_{ABC}=AB+AC+BC=4+4\sqrt{2}\)

Xét ΔABC có \(CA^2+CB^2=AB^2\)

nên ΔCAB vuông tại C

Diện tích tam giác ABC là:

\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}2\sqrt{2}\cdot2\sqrt{2}=\dfrac{1}{2}\cdot8=4\)

Số túi hạt sen đóng được nếu mỗi túi có 2kg là:

2430:2=1215(túi)

Số túi hạt sen đóng được nếu mỗi túi có 3kg là:

2430:3=810(túi)

Số túi hạt sen đóng được nếu mỗi túi có 5kg là:

2430:5=486(túi)

     Đây là dạng toán nâng cao chuyên đề vòi nước. Cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:

            Giải:

Cứ một giờ một mình vòi thứ nhất chảy được: 1 : 6 = \(\dfrac{1}{6}\) (bể)

Cứ một giờ vòi hai chảy một mình được: 1 : 4 = \(\dfrac{1}{4}\) (bể)

Cứ một giờ vòi ba tháo được: 1 : 8 = \(\dfrac{1}{8}\) (bể)

Khi cả ba vòi cùng mở thì chảy được: \(\dfrac{1}{6}+\dfrac{1}{4}-\dfrac{1}{8}=\dfrac{7}{24}\) (bể)

Kho bể cạn, cả ba vòi cùng chảy được: 1 : \(\dfrac{7}{24}\) = \(\dfrac{24}{7}\) (giờ)

Đáp số: \(\dfrac{24}{7}\) giờ. 

Số tiền cả gốc lẫn lãi người đó thu được:

50000000 + 50000000 × 0,65% × 12 = 50650000 (đồng)

Sau một năm người đó thu được số tiền cả gốc lẫn lãi là:

      50 000 000 x 0.65% = 50325000 (đồng)

a) Số phần quãng đường hai ngày sửa được:

5/14 + 2/7 = 9/14

b) Số phần quãng đường còn lại cần phải sửa:

1 - 9/14 = 5/14

Số m đường đội còn phải sửa:

1400 × 5/14 = 500 (m)

a: Cả hai ngày sửa được:

\(\dfrac{5}{14}+\dfrac{2}{7}=\dfrac{9}{14}\)(quãng đường)

b: Độ dài quãng đường còn lại mà đội phải sửa là:

\(1400\times\left(1-\dfrac{9}{14}\right)=1400\times\dfrac{5}{14}=500\left(m\right)\)

a: 24,75:0,25+24,75x724,75

=24,75x4+24,75x724,75

=24,75x(4+724,75)

=24,75x728,75

=18036,5625

b: Sửa đề: 41,82:0,2+41,82x6-41,82

=41,82x5+41,82x6-41,82

=41,82x(5+6)-41,82

=41,82x11-41,82

=41,82x10=418,2

1h12p=1,2 giờ 1h30p=1,5 giờ

Trong 1 giờ, vòi 1 và vòi2  chảy được: \(\dfrac{1}{1,2}=\dfrac{5}{6}\)(bể)

Trong 1 giờ, vòi 2 và vòi 3 chảy được: \(\dfrac{1}{2}\left(bể\right)\)

Trong 1 giờ, vòi 1 và vòi3  chảy được: \(\dfrac{1}{1,5}=\dfrac{2}{3}\)(bể)

Trong 1 giờ, ba vòi chảy được: \(\left(\dfrac{5}{6}+\dfrac{1}{2}+\dfrac{2}{3}\right):2=\left(\dfrac{5}{6}+\dfrac{3}{6}+\dfrac{4}{6}\right):2=\dfrac{12}{6}:2=1\left(bể\right)\)

13:

a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có

\(\widehat{HCA}\) chung

Do đó: ΔHAC~ΔABC

b: ΔHAC~ΔABC

=>\(\dfrac{CH}{CA}=\dfrac{CA}{CB}\)

=>\(CH\cdot CB=CA^2\)

c: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)

ΔHAC~ΔABC

=>\(\dfrac{HA}{AB}=\dfrac{CA}{CB}\)

=>\(HA=\dfrac{AB\cdot AC}{BC}=\dfrac{9\cdot12}{15}=9\cdot\dfrac{4}{5}=7,2\left(cm\right)\)

a: Xét ΔAMD và ΔCMB có

MA=MC

\(\widehat{AMD}=\widehat{CMB}\)

MD=MB

Do đó: ΔAMD=ΔCMB

b: Xét ΔMAB và ΔMCD có

MA=MC

\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)

MB=MD

Do đó: ΔMAB=ΔMCD
=>AB=CD

ΔMAB=ΔMCD

=>\(\widehat{MAB}=\widehat{MCD}\)

=>AB//CD

c: TA có: \(AN=\dfrac{AB}{2}\)

\(CE=\dfrac{CD}{2}\)

mà AB=CD

nên AN=CE

Xét ΔMAN và ΔMCE có

MA=MC

\(\widehat{MAN}=\widehat{MCE}\)

AN=CE
DO đó: ΔMAN=ΔMCE

=>\(\widehat{AMN}=\widehat{CME}\)

mà \(\widehat{AMN}+\widehat{NMC}=180^0\)(hai góc kề bù)

nên \(\widehat{CME}+\widehat{NMC}=180^0\)

=>N,M,E thẳng hàng

mà NM=ME(ΔMAN=ΔMCE)

nên M là trung điểm của NE