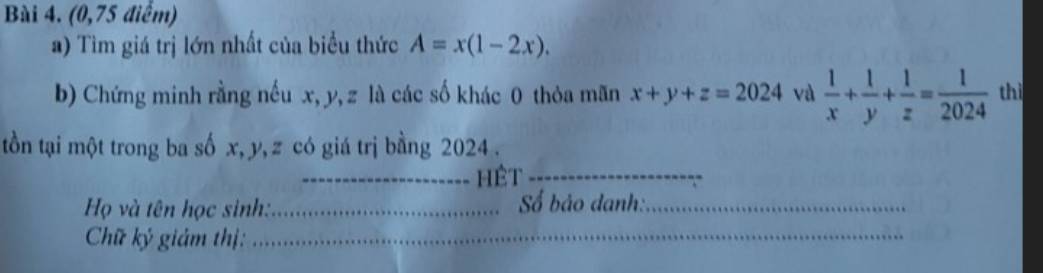a: Xét ΔBHA vuông tại H và ΔBFC vuông tại F có

\(\widehat{HBA}=\widehat{FBC}\)

Do đó: ΔBHA~ΔBFC

=>\(\dfrac{BH}{BF}=\dfrac{BA}{BC}\)

=>\(BH\cdot BC=BA\cdot BF\)

Xét ΔBAC có BE là phân giác

nên \(\dfrac{EA}{EC}=\dfrac{BA}{BC}=\dfrac{8}{5}\)

    Giải:

\(\dfrac{3}{5}\) số gạo trong thùng nặng là: \(\dfrac{175}{4}\) x \(\dfrac{3}{5}\) : \(\dfrac{7}{8}\) = 30 (kg)

Trong thùng có số gạo là:  \(\dfrac{175}{4}\) : \(\dfrac{7}{8}\) = 50 (kg)

Sau khi bán trong thùng còn lại số gạo là: 50 - 30 =  20 (kg)

Số gạo trong thùng có giá trị là: 15 000 x 20 =  300 000 (đồng)

Kết luận: Số gạo còn lại sau khi bán có giá trị là: 300 000 đồng.

a: Xét ΔAMB vuông tại M và ΔAKC vuông tại K có

\(\widehat{MAB}\) chung

Do đó: ΔAMB~ΔAKC

b: ΔAMB~ΔAKC

=>\(\dfrac{AM}{AK}=\dfrac{AB}{AC}\)

=>\(\dfrac{AM}{AB}=\dfrac{AK}{AC}\)

Xét ΔAMK và ΔABC có

\(\dfrac{AM}{AB}=\dfrac{AK}{AC}\)

\(\widehat{MAK}\) chung

Do đó: ΔAMK~ΔABC

=>\(\widehat{AMK}=\widehat{ABC}\)

c: Xét ΔABC có

BM,CK là các đường cao

BM cắt CK tại H

Do đó: H là trực tâm của ΔABC

=>AH\(\perp\)BC tại D

Xét ΔBDH vuông tại D và ΔBMC vuông tại M có

\(\widehat{DBH}\) chung

Do đó: ΔBDH~ΔBMC

=>\(\dfrac{BD}{BM}=\dfrac{BH}{BC}\)

=>\(BH\cdot BM=BD\cdot BC\)

Xét ΔCDH vuông tại D và ΔCKB vuông tại K có

\(\widehat{DCH}\) chung

Do đó: ΔCDH~ΔCKB

=>\(\dfrac{CD}{CK}=\dfrac{CH}{CB}\)

=>\(CD\cdot CB=CH\cdot CK\)

\(BH\cdot BM+CH\cdot CK\)

\(=BD\cdot BC+CD\cdot BC=BC\left(BD+CD\right)=BC^2\)

Gọi giá tiền người đó phải trả nếu mua vào thời điểm trước ngày chủ nhật là x(đồng)

(Điều kiện: x>0)

Giá tiền người đó phải trả nếu mua vào ngày chủ nhật là:

\(x\left(1+20\%\right)=1,2x\left(đồng\right)\)

Giá tiền người đó phải trả nếu mua vào ngày thứ hai là:

\(1,2x\left(1-0,2\right)=0,96x\left(đồng\right)\)

Do đó, ta có phương trình:

0,96x=24000

=>x=25000(nhận)

vậy: giá tiền người đó phải trả nếu mua vào thời điểm trước ngày chủ nhật là 25000(đồng)

a.

\(A=x\left(1-2x\right)=-2x^2+x=-2\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{8}\le\dfrac{1}{8}\)

\(A_{max}=\dfrac{1}{8}\) khi \(x=\dfrac{1}{2}\)

b.

\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{1}{x+y+z}\) (do \(x+y+z=2024\))

\(\Rightarrow\dfrac{x+y}{xy}+\dfrac{1}{z}-\dfrac{1}{x+y+z}=0\)

\(\Rightarrow\dfrac{x+y}{xy}+\dfrac{x+y}{z\left(x+y+z\right)}=0\)

\(\Rightarrow\left(x+y\right)\left(\dfrac{1}{xy}+\dfrac{1}{z\left(x+y+z\right)}\right)=0\)

\(\Rightarrow\left(x+y\right)\left(\dfrac{xy+xz+yz+z^2}{xyz\left(x+y+z\right)}\right)=0\)

\(\Rightarrow\left(x+y\right)\left(\dfrac{x\left(y+z\right)+z\left(y+z\right)}{xyz\left(x+y+z\right)}\right)=0\)

\(\Rightarrow\dfrac{\left(x+y\right)\left(y+z\right)\left(x+z\right)}{xyz\left(x+y+z\right)}=0\)

\(\Rightarrow\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x+y=0\\y+z=0\\x+z=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x+y+z=z\\x+y+z=x\\x+y+z=y\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}2024=z\\2024=x\\2024=y\end{matrix}\right.\) (đpcm)

Gọi giá 1kWh ở mức 1 là x(đồng)

(ĐK: x>0)

Giá 1kWh ở mức 2 là x+56(đồng)

Giá 1kWh ở mức 3 là x+56+280=x+336(đồng)

Số kWh ở mức 3 sử dụng là:

131-50-50=31(kWh)

Số tiền phải trả cho 50kWh ở mức 1 là 50x(đồng)

Số tiền phải trả cho 50kWh ở mức 2 là 50(x+56)(đồng)

Số tiền phải trả cho 31kWh ở mức 3 là 31(x+336)(đồng)

Do đó, ta có phương trình:

50x+50(x+56)+31(x+336)=233034

=>131x+13216=233034

=>131x=219818

=>x=1678(nhận)

Vậy: Giá 1kWh ở mức 1 là 1678 đồng

Thể tích nước trong bể là:

12x4,5x1,5=18x4,5=81(m³)