=17,49

3/16 + 14/33

= 99/528  + 224/528

= 323/528

Lời giải:

* $m$ phải là số tự nhiên khác 0 bạn nhé.
$(m:1-m\times 1):(m\times 1991+m\times 1)$

$=(m-m): (m\times 1991+m\times 1)=0:(m\times 1991+m\times 1)=0$

a.

Nửa chu vi thửa ruộng là:

\(54:2=27\left(m\right)\)

Chiều dài thửa ruộng là:

\(\left(27+3\right):2=15\left(m\right)\)

Chiều rộng thửa ruộng là:

\(\left(27-3\right):2=12\left(m\right)\)

Diện tích thửa ruộng là:

\(15\times12=180\left(m^2\right)\)

b.

Số kilogam thóc thu hoạch được là:

\(180\times\dfrac{5}{2}:1=450\left(kg\right)\)

                                             Giải

                          Chiều dài thửa ruộng đó là

                                   (54+3):2=28,5(m)

                           Chiều rộng thửa ruộng đó là:

                                    54-28,5=25,5(m)

                            a)Diện tích thửa ruộng đó là:

                                    25,5x28,5=726,75(m²)

                             b)Cả thửa ruộng đó có số thóc là:

                                     5/2 x (726,75 :1)=1816,875(kg)

                                                   Đáp số:a) 726,75m²

                                                                b)1816,875kg thóc

cần bớt 0,1 đơn vị

2/3 nha các anh

Ta có:

\(A^2=\dfrac{x^2y^2}{z^2}+\dfrac{y^2z^2}{x^2}+\dfrac{z^2x^2}{y^2}+2x^2+2y^2+2z^2\)

\(\Rightarrow A^2=\dfrac{x^2y^2}{z^2}+\dfrac{y^2z^2}{x^2}+\dfrac{z^2x^2}{y^2}+2\) (1)

Mặt khác:

\(\dfrac{x^2y^2}{z^2}+\dfrac{y^2z^2}{x^2}\ge2\sqrt{\dfrac{x^2z^2y^4}{z^2x^2}}=2y^2\)

Tương tự: \(\dfrac{x^2y^2}{z^2}+\dfrac{z^2x^2}{y^2}\ge2x^2\) ; \(\dfrac{y^2z^2}{x^2}+\dfrac{z^2x^2}{y^2}\ge2z^2\)

Cộng vế \(\Rightarrow\dfrac{x^2y^2}{z^2}+\dfrac{z^2x^2}{y^2}+\dfrac{x^2y^2}{z^2}\ge x^2+y^2+z^2=1\) (2)

Từ (1);(2) \(\Rightarrow A^2\ge1+2=3\)

\(\Rightarrow A\ge\sqrt{3}\)

Dấu "=" xảy ra khi \(x=y=z=\dfrac{1}{\sqrt{3}}\)

"hai so co nhieu bang 32" nghĩa là sao hả bạn?

Số lớn: 41

Số bé: 9

41: 9 = 4 (dư 5)

41- 9 = 32

Tick cho mik nhé:)

1=4,5

2=32,0444

3=2,5

4= -51,9437

thế này mà là lớp 1 á

Lời giải:

Tổng của $a$ và $b$: $432\times 2=864$

Tổng của $b$ và $c$: $421\times 2=842$

Tổng của số $a$ và $c$: $368\times 2=736$

Tổng của ba số $a,b,c$: $(864+842+736):2=1221$

Trung bình cộng của 3 số là: $1221:3=407$

TBC cộng của 3 số abc là 407

Giá chiếc lò vi sóng sau khi giảm 20% là:

\(1\text{ }250\text{ }000.\left(100\%-20\%\right)=1\text{ }000\text{ }000\) (đồng)

Bác Hoa phải trả số tiền là:

\(1\text{ }000\text{ }000.\left(100\%-10\%\right)=900\text{ }000\) (đồng)

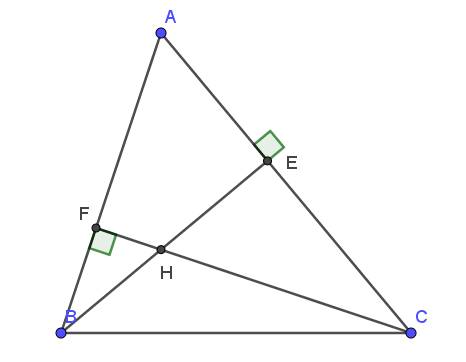
Lời giải:

a. Xét tam giác $AEB$ và $AFC$ có:

$\widehat{A}$ chung

$\widehat{AEB}=\widehat{AFC}=90^0$

$\Rightarrow \triangle AEB\sim \triangle AFC$ (g.g)

b.

Xét tam giác $HFB$ và $HEC$ có:

$\widehat{FHB}=\widehat{EHC}$ (đối đỉnh)

$\widehat{HFB}=\widehat{HEC}=90^0$

$\Rightarrow \triangle HFB\sim \triangle HEC$ (g.g)

$\Rightarrow \frac{HF}{HB}=\frac{HE}{HC}\Rightarrow HF.HC=HB.HE$ 

c.

Từ kết quả phần a suy ra $\frac{AE}{AF}=\frac{AB}{AC}$

Xét tam giác $ABC$ và $AEF$ có:

$\widehat{A}$ chung

$\frac{AB}{AC}=\frac{AE}{AF}$

$\Rightarrow \triangle ABC\sim \triangle AEF$ (c.g.c)

Hình vẽ: