cho tam giác abc cân tại A B là trung điểm của BC các đường trung tuyến của AB AC cắt nhau tại D a) chứng minh A,M,D thẳng hàng b) chứng minh tam giác ABM = tam giác ACM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt : \(\dfrac{x}{3}=\dfrac{y}{6}=k\)
=> x = 3k; y = 6k
Ta có : 4x - y = 42
=> 4.3k - 6k = 42
=> 12k - 6k = 42
=> 6k = 42
=> k = 7
=> x = 3 . 7 = 21
\(\dfrac{x}{3}=\dfrac{y}{6}\Rightarrow y=2x\Rightarrow x=\dfrac{y}{2}\)
\(4x-y=42\)
\(4\cdot\dfrac{y}{2}-y=42\)
\(y\left(4\cdot\dfrac{1}{2}-1\right)=42\)
\(y\cdot1=42\)
\(y=42\Rightarrow x=\dfrac{42}{2}=21\)

a/
Xét tg ACK có
\(CH\perp AK;AN\perp CK\) => M là trực tâm của tg ACK
\(\Rightarrow KM\perp AC\) mà \(AB\perp AC\) => KM//AB (cùng vuông góc với AC)
Xét tg vuông ABH và tg vuông KMH có
KM//AB => \(\widehat{ABH}=\widehat{KMH}\) (góc so le trong)
HB=HM (gt)
=> tg ABH = tg KMH (Hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau) => KM=AB
b/
Ta có tg ABH = tg KMH (cmt) => AH=KH => CH là trung tuyến của tg CKA
Ta có CH là đường cao của tg CKA
=> tg CKA cân tại C (trong tg đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
c/
Tg CKA là tg đều \(\Rightarrow\widehat{ACK}=60^o\)
Ta có CH là phân giác của \(\widehat{ACK}\) (trong tg cân đường cao đồng thời là đường phân giác)
\(\Rightarrow\widehat{ACB}=\widehat{KCH}=30^o\)
Vậy để tg CKA là tg đều thì tg ABC phải cần đk là \(\widehat{ACB}=30^o\)


Có : \(\widehat{ACB}+\widehat{A'CB'}=60^0\)
Mà \(\widehat{ACB}=\widehat{A'CB'}\) (2 góc đối đỉnh )
=>\(\widehat{ACB}=\widehat{A'CB'}=\dfrac{60}{2}=30^0\)
Ta có \(\widehat{ACB}+\widehat{BCA'}=180^0\) (2 góc kề bù )
=> \(\widehat{BCA'}=180^0-\widehat{ACB}=180^0-30^0=150^0\)

\(\dfrac{x}{3}=\dfrac{y}{3}\Rightarrow\dfrac{4x}{12}=\dfrac{y}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{4x}{12}=\dfrac{y}{3}=\dfrac{4x-y}{12-3}=\dfrac{42}{9}=\dfrac{14}{3}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{14}{3}\Rightarrow x=14\\\dfrac{y}{3}=\dfrac{14}{3}\Rightarrow y=14\end{matrix}\right.\)

\(b,\)
\(27^2:25^3=\left(3^3\right)^2:\left(5^2\right)^3=3^6:5^6=\left(\dfrac{3}{5}\right)^6\)
\(c,\)
\(25^4.2^8=\left(5^2\right)^4.2^8=5^8.2^8=\left(5.2\right)^8.10^8\)
\(d,\)
\(32^4.64^3=\left(2^5\right)^4.\left(2^6\right)^3=2^{20}.2^{18}=2^{38}\)
\(25^3:5^2=\left(5^2\right)^3:5^2=\left(5^2\right)^2=5^4\)
\(e,\)
\(64^2.16^4=\left(2^6\right)^2.\left(2^4\right)^4=2^{12}.2^{16}=2^{28}\)
\(625^5.5^3=\left(5^4\right)^5:5^3=5^{20}:5^3=5^{17}\)


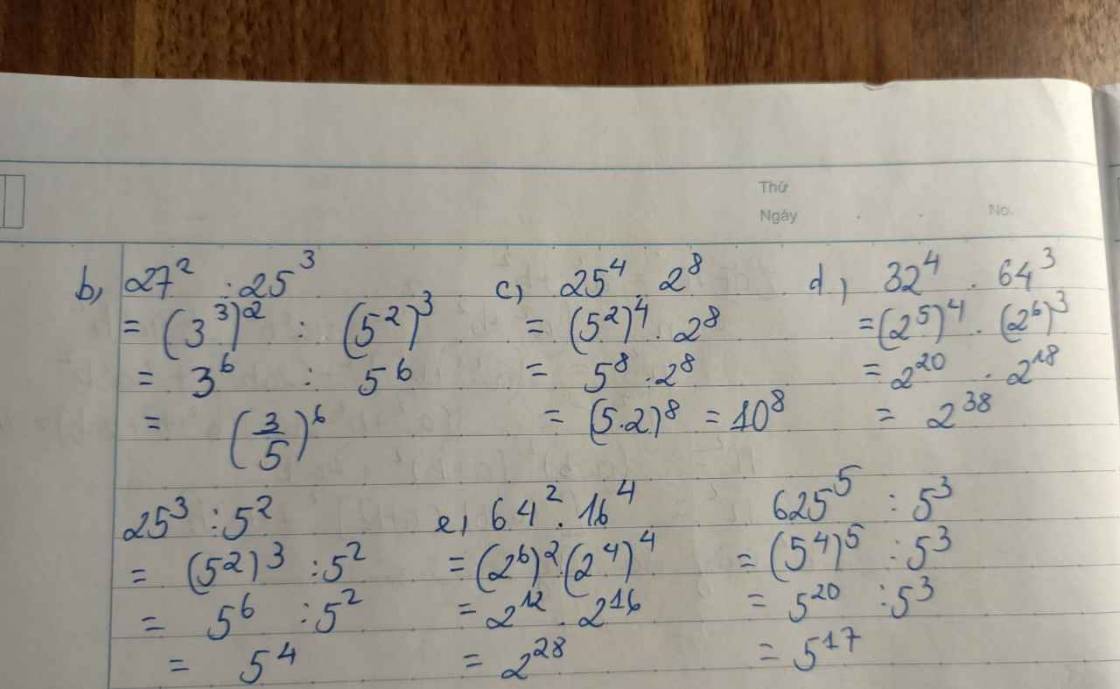
Bài này bạn đã đăng rồi thì hạn chế không đăng lại, tránh gây spam.