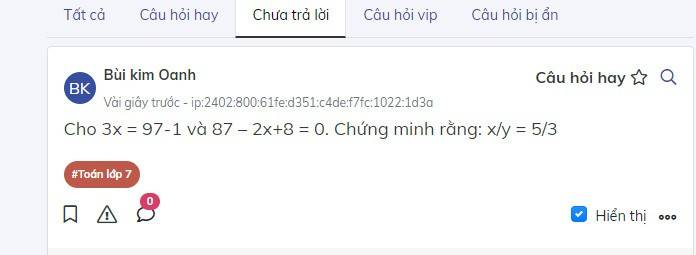
Cho 3x = 97-1 và 87 – 2x+8 = 0. Chứng minh rằng: x/y = 5/3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Chiều cao của khối rubik là:
\(44,002\cdot3:22,45=5,88\left(cm\right)\)
2:
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BH\cdot BC\)
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{18^2+24^2}=30\left(cm\right)\)
Xét ΔCAB có CD là phân giác
nên \(\dfrac{DA}{AC}=\dfrac{DB}{BC}\)
=>\(\dfrac{DA}{24}=\dfrac{DB}{30}\)
=>\(\dfrac{DA}{4}=\dfrac{DB}{5}\)
mà DA+DB=AB=18cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DA}{4}=\dfrac{DB}{5}=\dfrac{DA+DB}{4+5}=\dfrac{18}{9}=2\)
=>\(DA=4\cdot2=8\left(cm\right)\)

\(\dfrac{2x-5}{x-1}\) nguyên
⇒ \(\left(2x-5\right)⋮\left(x-1\right)\)
Mà \(\left(x-1\right)⋮\left(x-1\right)\)
⇒ \(\left[\left(2x-5\right)-\left(x-1\right)-\left(x-1\right)\right]⋮\left(x-1\right)\)
⇒ \(\left(-3\right)⋮\left(x-1\right)\)
⇒ \(\left(x-1\right)\inƯ\left(-3\right)\)
\(\in\left\{1;3;-1;-3\right\}\)
| \(x-1\) | 1 | 3 | -1 | -3 |
| \(x\) | 2 | 4 | 0 | -2 |
Vậy \(x\in\left\{-2;0;2;4\right\}\)

a: Vì \(\dfrac{6}{12}=\dfrac{9}{18}=\dfrac{12}{24}\left(=\dfrac{1}{2}\right)\)
nên hai tam giác này đồng dạng với nhau
b: Vì \(\dfrac{AB}{DE}=\dfrac{AC}{DF}\ne\dfrac{BC}{EF}\)
nên hai tam giác này không đồng dạng với nhau

Câu 5:
Gọi hàm số bậc nhất cần tìm có dạng là y=ax+b(\(a\ne0\))
Vì đồ thị hàm số y=ax+b song song với đường thẳng y=-2x+1 nên \(\left\{{}\begin{matrix}a=-2\\b\ne1\end{matrix}\right.\)
Vậy: y=-2x+b
Thay x=-1 và y=3 vào y=-2x+b, ta được:
\(\left(-2\right)\cdot\left(-1\right)+b=3\)
=>b+2=3
=>b=1(loại)
Vậy: KHông có hàm số bậc nhất nào thỏa mãn yêu cầu đề bài
Câu 4:
Gọi hàm số bậc nhất cần tìm có dạng là y=ax+b(\(a\ne0\))
Vì đồ thị hàm số y=ax+b song song với đường thẳng y=-2x+1 nên \(\left\{{}\begin{matrix}a=-2\\b\ne1\end{matrix}\right.\)
Vậy: y=-2x+b
Thay x=-1 và y=4 vào y=-2x+b, ta được:
\(\left(-2\right)\cdot\left(-1\right)+b=4\)
=>b+2=4
=>b=2(nhận)
vậy: y=-2x+2

Vì số chia là 4 nên số chia chỉ có thể là: 0; 1; 2; 3

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
=>HM=HN
c: ΔAMH=ΔANH
=>AM=AN
=>A nằm trên đường trung trực của MN(1)
Ta có: HM=HN
=>H nằm trên đường trung trực của NM(2)
Từ (1),(2) suy ra AH là đường trung trực của NM
=>AH\(\perp\)NM
d: Xét ΔAPQ có
PN,QM là các đường cao
PN cắt QM tại H
Do đó: H là trực tâm của ΔAPQ
=>AH\(\perp\)PQ tại E
Xét tứ giác AMHN có \(\widehat{AMH}+\widehat{ANH}=90^0+90^0=180^0\)
nên AMHN là tứ giác nội tiếp
Xét tứ giác HMPE có \(\widehat{HMP}+\widehat{HEP}=90^0+90^0=180^0\)
nên HMPE là tứ giác nội tiếp
Xét tứ giác HNQE có \(\widehat{HNQ}+\widehat{HEQ}=90^0+90^0=180^0\)
nên HNQE là tứ giác nội tiếp
Ta có: \(\widehat{MEH}=\widehat{MPH}\)(MHEP nội tiếp)
\(\widehat{NEH}=\widehat{NQH}\)(NHEQ nội tiếp)
mà \(\widehat{MPH}=\widehat{NQH}\left(=90^0-\widehat{PAQ}\right)\)
nên \(\widehat{MEH}=\widehat{NEH}\)
=>EH là phân giác của góc MEN
Ta có: \(\widehat{NMH}=\widehat{NAH}\)(AMHN nội tiếp)
\(\widehat{EMH}=\widehat{EPH}\)(MHEP nội tiếp)
mà \(\widehat{NAH}=\widehat{EPH}\left(=90^0-\widehat{AQP}\right)\)
nên \(\widehat{NMH}=\widehat{EMH}\)
=>MH là phân giác của góc NME
Xét ΔNME có
MH,EH là các đường phân giác
Do đó: H là tâm đường tròn nội tiếp ΔNME
=>H là điểm cách đều ba cạnh của ΔMNE

Đây là dạng toán tổng tỉ ần tỉ, cấu trúc thi học sinh giỏi, thi violympic, thi học sinh giỏi các cấp. Hôm nay, Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Số lớn bằng: 1 + \(\dfrac{1}{4}\) = \(\dfrac{5}{4}\) (số bé)
Ta có sơ đồ:
Theo sơ đồ ta có:
Số bé là: 180 : (4 + 5) x 4 = 80
Số lớn là: 180 - 80 = 100
Đáp số: số lớn là: 100
số bé là 80

M thuộc đoạn $AB$, mà $AM=AB$? Bạn xem lại đề nhé. Như thế này thì $M$ trùng $B$ rồi.

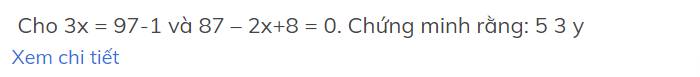


3\(x\) = 97 - 1
3\(x\) = 96
\(x\) = 96 : 3
\(x\) = 32
87 - 2\(x\) + 8 = 0
95 - 2\(x\) = 0
2\(x\) = 95
\(x\) = \(\dfrac{95}{2}\) ≠ 32
Không tồn tại \(x\) thỏa mãn đề bài.