PT: \(CaCO_3\underrightarrow{t^o}CaO+CO_2\)

Theo ĐL BTKL, có: m_CaCO3 = m_CaO + m_CO2 = 44,8 + 35,2 = 80 (g)

\(\Rightarrow\%CaCO_3=\dfrac{80}{400}.100\%=20\%\) = x

1)

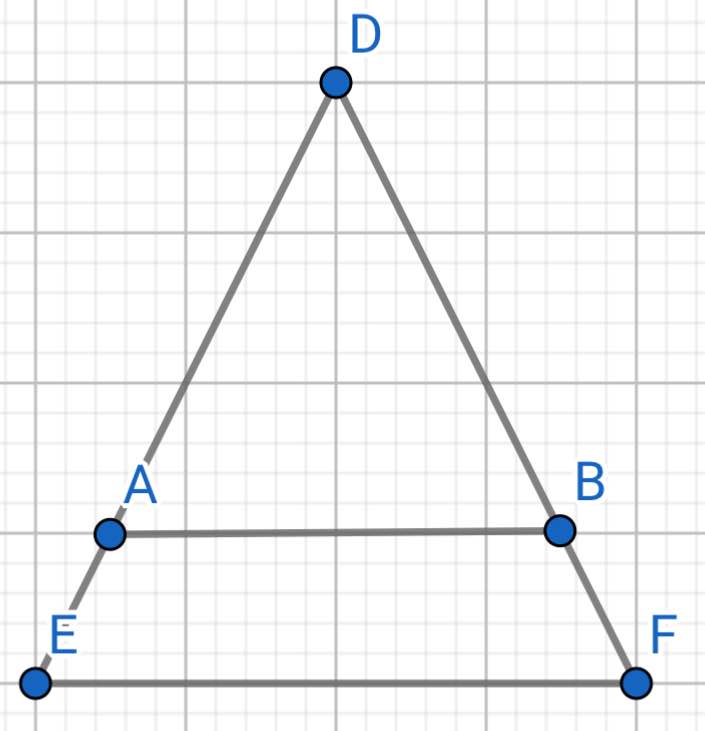
a) Do tam giác DEF cân tại D (gt)

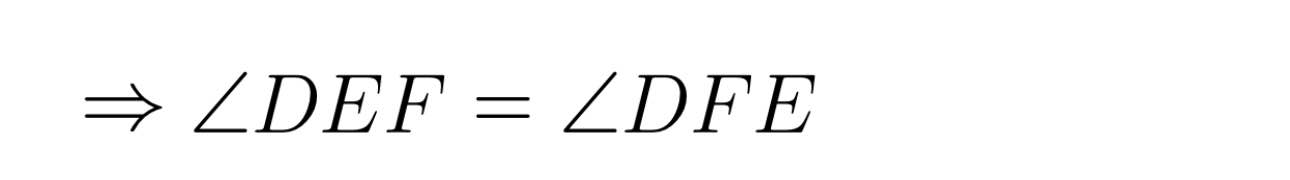
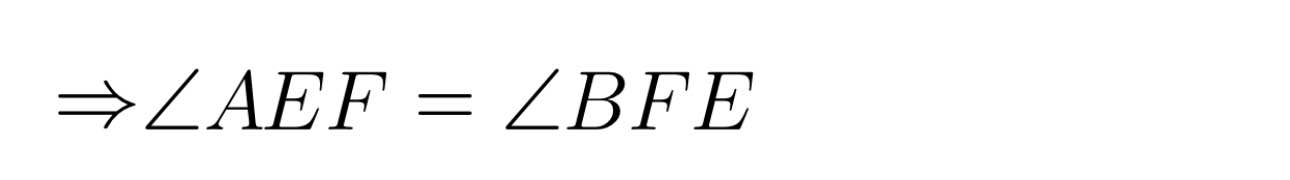
Tam giác DAB có:

DA = DB (gt)

=> Tam giác DAB cân tại D

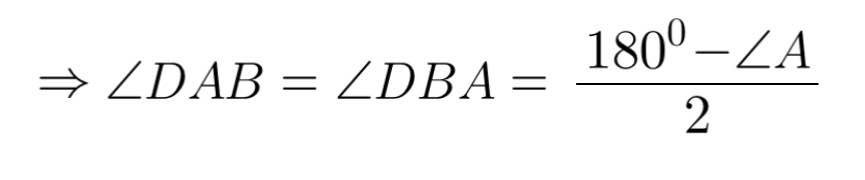
Do tam giác DEF cân tại D (gt)

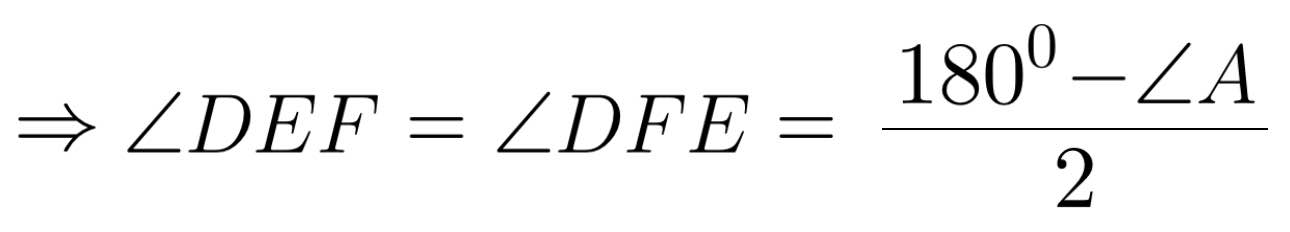
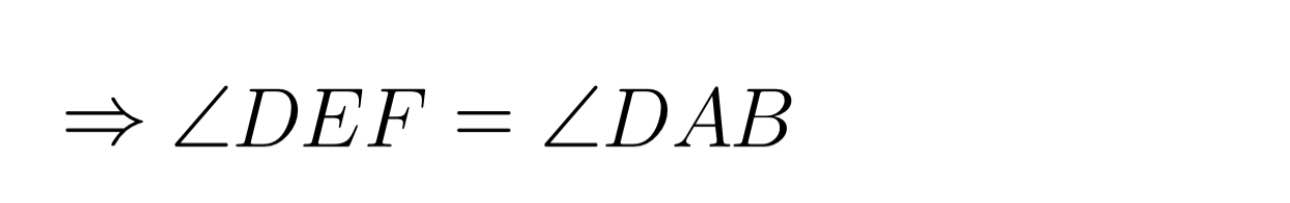
Mà góc DEF và góc DAB đồng vị

=> EABF là hình thang

Mà:

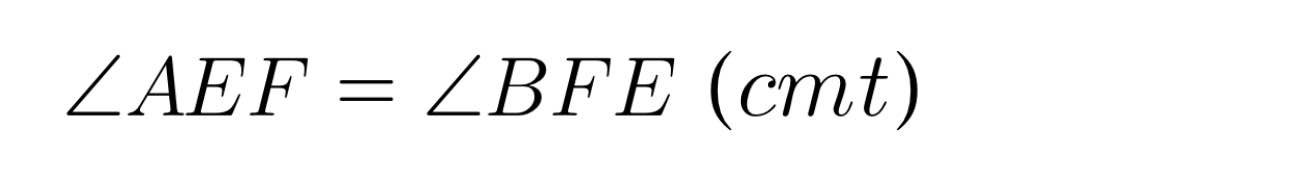
=> EABF là hình thang cân

b) Do tam giác DEF cân tại D (gt)

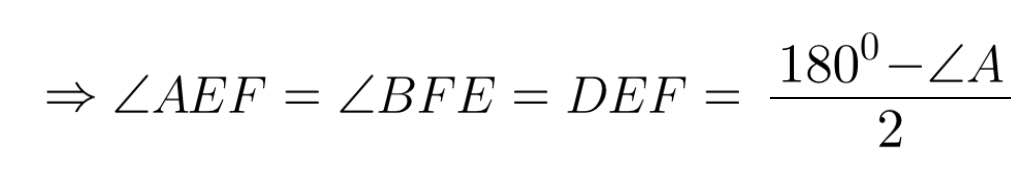
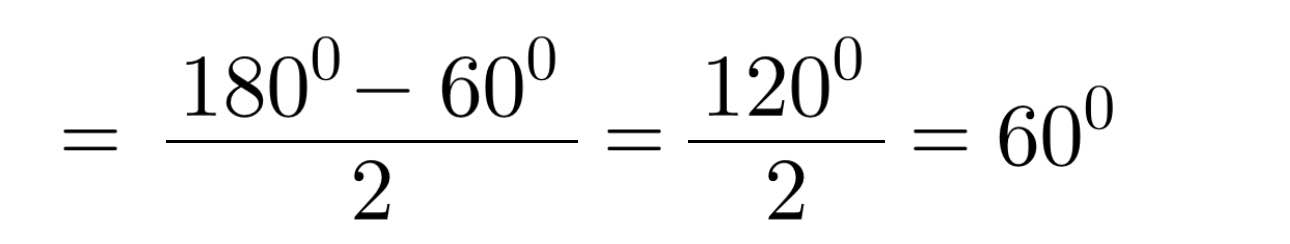
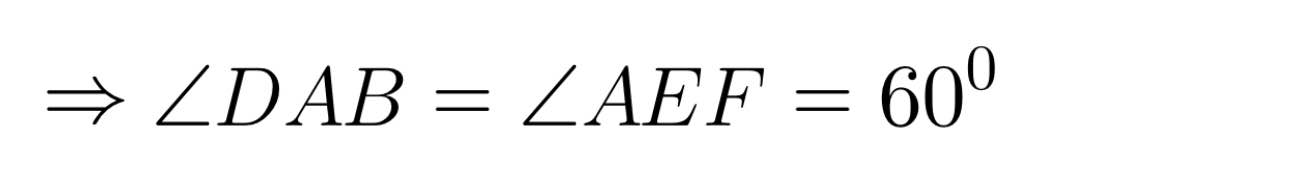
Ta có:

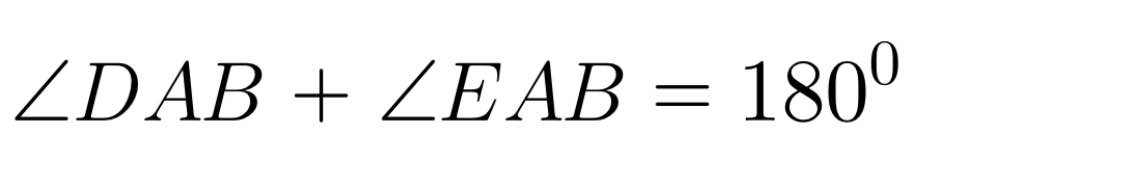
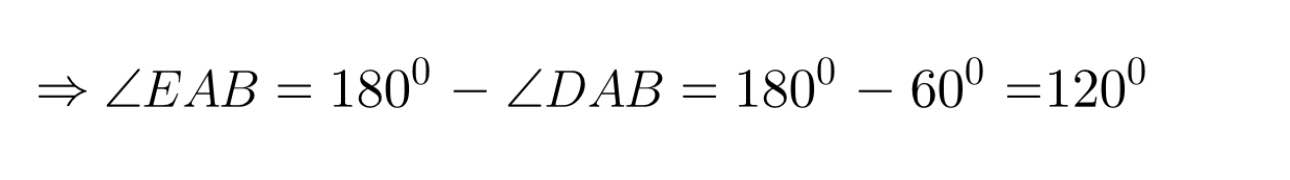
Bài 3

Tam giác ABD có:

AB = AD (gt)

=> Tam giác ABD cân tại A

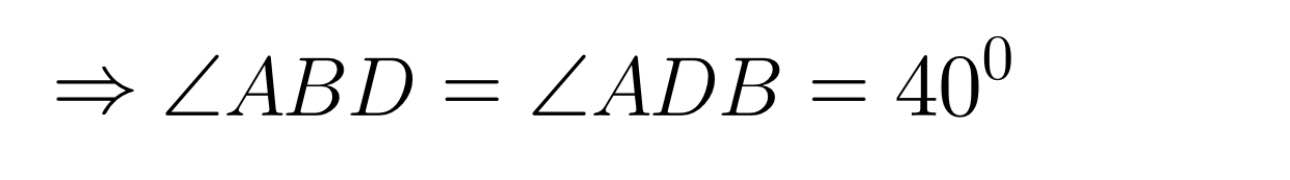
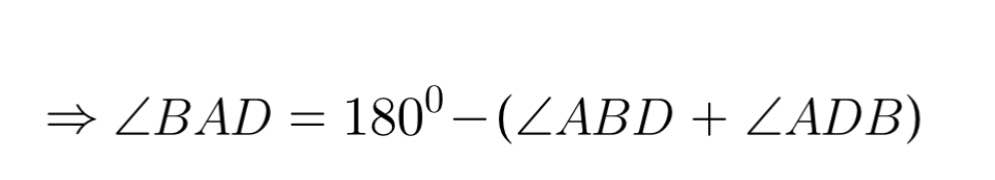
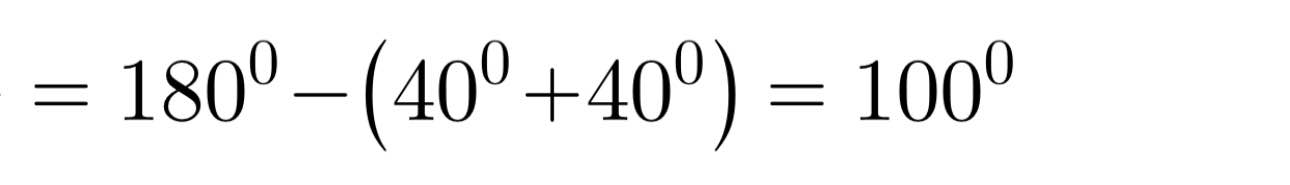
Ta có:

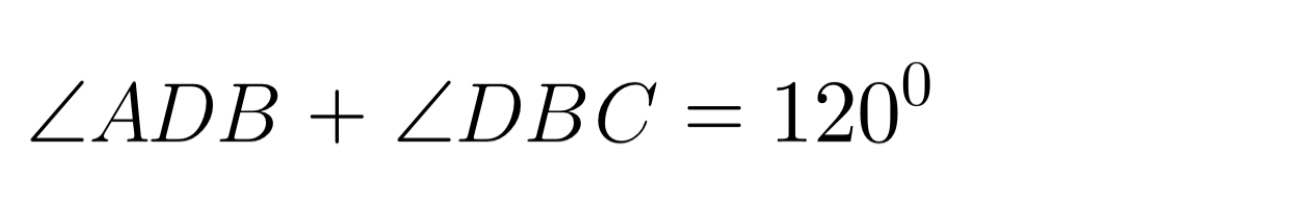
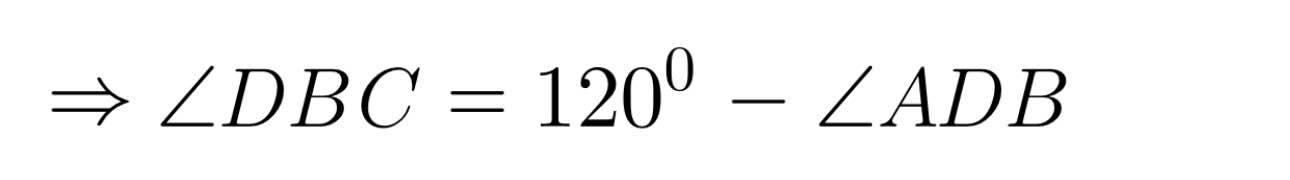
= 120⁰ − 40⁰

= 80⁰

Tam giác BCD có:

CB = CD (gt)

=> Tam giác BCD cân tại C

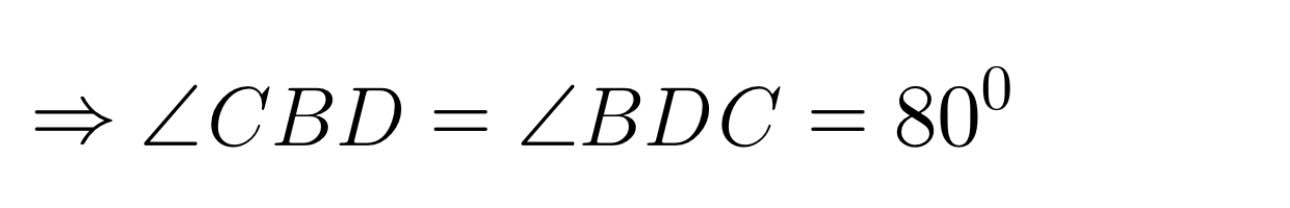
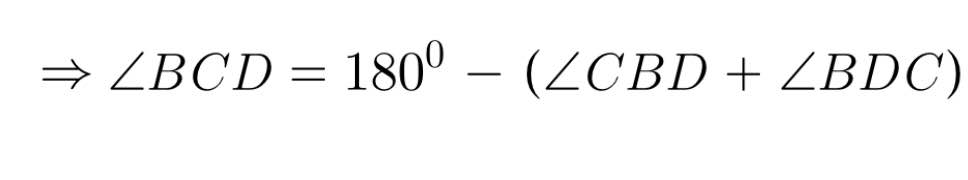
= 180⁰ − (80⁰ + 80⁰) = 20⁰

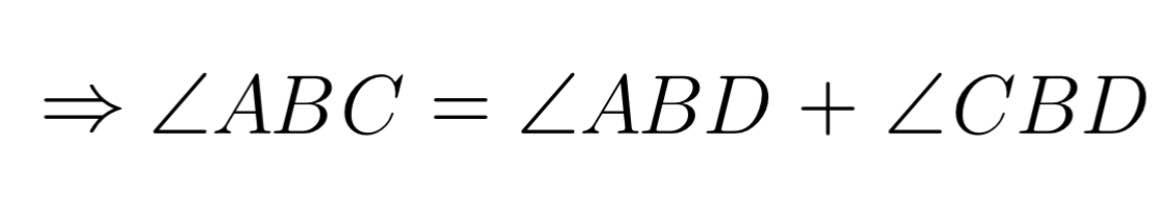
= 40⁰ + 40⁰

= 80⁰

Công thức câu bị động:

→ O + tobe + Vpp + (by S)

Ta có cách chuyển từ câu chủ động sang câu bị động như sau: 

☘ Bạn tham khảo:

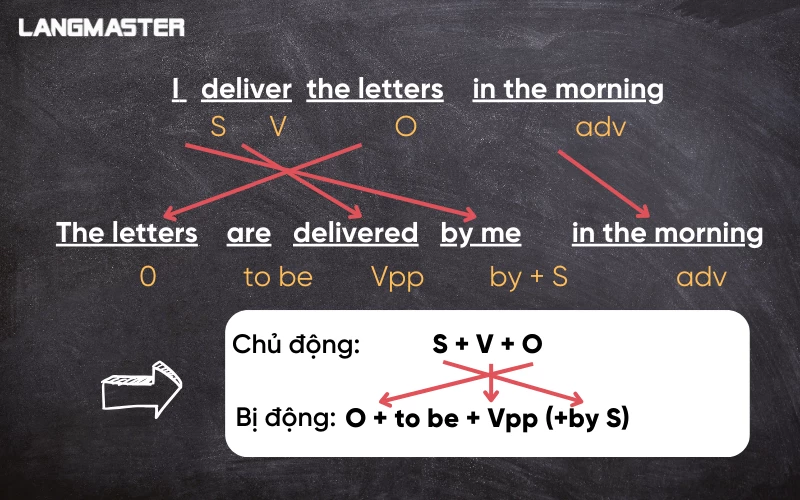
Bước 1: Xác định tân ngữ trong câu (O) và đẩy lên đầu câu làm chủ ngữ (S).

Bước 2: Quan sát động từ chính (V) và xác định thì của câu. 

Bước 3: Chuyển đổi động từ về dạng bị động “to be + Vpp” theo thì của câu gốc

Lưu ý: To be của câu bị động  => chia theo V trong câu chủ động 

Bước 4: Chuyển đổi chủ ngữ (S) trong câu chủ động thành tân ngữ (O), đưa về cuối câu và thêm “by” phía trước.

\(P\left(x-1\right)=\left(x^2-2x+1\right)-\left(2x-2\right)+3=\left(x-1\right)^2-2\left(x-1\right)+3\)

\(\Rightarrow P\left(x\right)=x^2-2x+3\)

Cảm ơn bạn 

\(\left(x+1\right)\left(x-1\right)-\left(x+1\right)\\ =x^2-1^2-x-1\\ =x^2-1-x-1\\ =x^2-x-2\)

Phân tích đa thức hay như nào em ơi?

A = (\(x\) + 1)(\(x-1\)) - (\(x+1\))

A = (\(x+1\))(\(x-1\) - 1)

A = (\(x+1\))(\(x\) - 2)

a: Xét ΔDBE vuông tại D và ΔCDE vuông tại C có

\(\widehat{DEB}\) chung

Do đó: ΔDBE~ΔCDE

b:

Ta có: CH\(\perp\)DE

DB\(\perp\)DE

Do đó: CH//DB

Xét ΔHCD vuông tại H và ΔCDB vuông tại C có

\(\widehat{HCD}=\widehat{CDB}\)(hai góc so le trong, CH//DB)

Do đó: ΔHCD~ΔCDB

=>\(\dfrac{HC}{CD}=\dfrac{CD}{DB}\)

=>\(HC\cdot DB=CD^2\)

c: ABCD là hình chữ nhật

=>AC cắt BD tại trung điểm của mỗi đường

=>O là trung điểm của BD

=>OB=OD(1)

Xét ΔEOD có HK//OD

nên \(\dfrac{HK}{OD}=\dfrac{EK}{EO}\left(2\right)\)

Xét ΔEOB có KC//OB

nên \(\dfrac{KC}{OB}=\dfrac{EK}{EO}\left(3\right)\)

Từ (1),(2),(3) suy ra HK=KC

=>K là trung điểm của HC

4x+3y-xy=1

=>\(4x-xy+3y=1\)

=>\(x\left(4-y\right)+3y-12=-11\)

=>-x(y-4)+3(y-4)=-11

=>(-x+3)(y-4)=-11

=>(x-3)(y-4)=11

=>\(\left(x-3;y-4\right)\in\left\{\left(1;11\right);\left(11;1\right);\left(-1;-11\right);\left(-11;-1\right)\right\}\)

=>\(\left(x;y\right)\in\left\{\left(4;15\right);\left(14;5\right);\left(2;-7\right);\left(-8;3\right)\right\}\)

a: Xét ΔAFH vuông tại F và ΔADB vuông tại D có

\(\widehat{FAH}\) chung

DO đó: ΔAFH~ΔADB

b: ΔAFH~ΔADB

=>\(\dfrac{AF}{AD}=\dfrac{AH}{AB}\)

=>\(\dfrac{AF}{AH}=\dfrac{AD}{AB}\)

Xét ΔAFD và ΔAHB có

\(\dfrac{AF}{AH}=\dfrac{AD}{AB}\)

\(\widehat{FAD}\) chung

Do đó: ΔAFD~ΔAHB

c: ΔAFD~ΔAHB

=>\(\widehat{ADF}=\widehat{ABH}\)

=>\(\widehat{ADF}=\widehat{ACH}\)

Xét ΔAEH vuông tại E và ΔADC vuông tại D có

\(\widehat{EAH}\) chung

DO đó: ΔAEH~ΔADC

=>\(\dfrac{AE}{AD}=\dfrac{AH}{AC}\)

=>\(\dfrac{AE}{AH}=\dfrac{AD}{AC}\)

Xét ΔAED và ΔAHC có

\(\dfrac{AE}{AH}=\dfrac{AD}{AC}\)

\(\widehat{EAD}\) chung

Do đó: ΔAED~ΔAHC

=>\(\widehat{ADE}=\widehat{ACH}\)

=>\(\widehat{FDA}=\widehat{EDA}\)

=>DA là phân giác của góc FDE