Câu 4. (1,5 điểm) Cho ABC có hai đường trung tuyến BM và CN bằng nhau và cắt nhau tai G. a) Chứng minh GB = GC. b) Chứng minh BON = COM c) Chứng minh ABC cân, chỉ rõ cân tại đâu. d) Gọi I là trung điểm BC. Chứng minh AI, BM, CN đồng quy.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 1,8m=18dm; 1,5m=15dm
Số lít nước hiện tại trong bể là:
\(18\times15\times12\times65\%=2106\left(lít\right)\)
b: Thể tích cần đổ thêm chiếm:
75%-65%=10%(bể)
Thể tích nước cần đổ thêm là:
\(18\times15\times12\times0,1=324\left(lít\right)\)

4,54x1,72+2,72x2x8,28+4,54
=4,54x(1,72+1)+5,44x8,28
=4,54x2,72+5,44x8,28
=4,54x2,72+2,72x16,56
=2,72x(4,54+16,56)
=2,72x21,1
=57,392
4,54x1,72+2,72x2x8,28+4,54
=4,54x(1,72+1)+5,44x8,28
=4,54x2,72+5,44x8,28
=4,54x2,72+2,72x16,56
=2,72x(4,54+16,56)
=2,72x21,1
=57,392
K ạ!

a: \(\dfrac{7}{6}\times\dfrac{9}{16}\times\dfrac{6}{7}\times16\)
\(=\dfrac{7}{6}\times\dfrac{6}{7}\times16\times\dfrac{9}{16}\)
\(=1\times9=9\)
b: \(\dfrac{7}{12}\times\dfrac{4}{9}+\dfrac{4}{9}\times\dfrac{5}{12}-\dfrac{2}{9}\)
\(=\dfrac{4}{9}\times\left(\dfrac{7}{12}+\dfrac{5}{12}\right)-\dfrac{2}{9}\)
\(=\dfrac{4}{9}-\dfrac{2}{9}=\dfrac{2}{9}\)

1: \(\dfrac{1}{2}-\left(\dfrac{2}{3}\right)^9:\left(\dfrac{2}{3}\right)^7+\dfrac{5}{6}\)
\(=\dfrac{1}{2}-\left(\dfrac{2}{3}\right)^2+\dfrac{5}{6}\)
\(=\dfrac{1}{2}-\dfrac{4}{9}+\dfrac{5}{6}\)
\(=\dfrac{9}{18}-\dfrac{8}{18}+\dfrac{15}{18}=\dfrac{16}{18}=\dfrac{8}{9}\)
2: \(\left(\dfrac{3}{7}\right)^3\cdot\left(\dfrac{7}{6}\right)^3+\dfrac{2}{3}:\left(\dfrac{4}{3}\right)^2\)
\(=\dfrac{1}{8}+\dfrac{2}{3}:\dfrac{16}{9}\)
\(=\dfrac{1}{8}+\dfrac{2}{3}\cdot\dfrac{9}{16}\)
\(=\dfrac{1}{8}+\dfrac{3}{8}=\dfrac{4}{8}=\dfrac{1}{2}\)
3: \(-\dfrac{4}{7}:\dfrac{9}{14}+\left(\dfrac{4}{3}\right)^4:\left(\dfrac{4}{3}\right)^2\)
\(=-\dfrac{4}{7}\cdot\dfrac{14}{9}+\left(\dfrac{4}{3}\right)^2\)
\(=-\dfrac{8}{9}+\dfrac{16}{9}=\dfrac{8}{9}\)
4: \(\left(-\dfrac{4}{3}+1\right)-\left(-\dfrac{2}{3}\right)^{21}:\left(-\dfrac{2}{3}\right)^{19}\)
\(=\dfrac{-1}{3}-\left(-\dfrac{2}{3}\right)^2\)
\(=-\dfrac{1}{3}-\dfrac{4}{9}=-\dfrac{7}{9}\)
5: \(\left(\dfrac{5}{2}-\dfrac{4}{3}\right)\cdot\dfrac{6}{7}+\left(-\dfrac{3}{2}\right)^5:\left(-\dfrac{3}{2}\right)^3\)
\(=\dfrac{15-8}{6}\cdot\dfrac{6}{7}+\left(-\dfrac{3}{2}\right)^2\)
\(=1+\dfrac{9}{4}=\dfrac{13}{4}\)
6: \(25^{10}\cdot\left(\dfrac{1}{5}\right)^{20}+\left(-\dfrac{3}{4}\right)^8\cdot\left(-\dfrac{4}{3}\right)^8-2011^0\)
\(=\dfrac{5^{20}}{5^{20}}+1-1=1+1-1=1\)
7: \(\left(\dfrac{3}{5}\right)^{10}\cdot\left(\dfrac{5}{3}\right)^{10}-\dfrac{13^4}{39^4}+2014^0\)
\(=\left(\dfrac{3}{5}\cdot\dfrac{5}{3}\right)^{10}-\dfrac{1}{3^4}+1\)
\(=1+1-\dfrac{1}{81}=2-\dfrac{1}{81}=\dfrac{161}{81}\)
8: \(\left(-0,5\right)^5:\left(-0,5\right)^3-\left(\dfrac{17}{2}\right)^7:\left(\dfrac{17}{2}\right)^6\)
\(=\left(-0,5\right)^2-\dfrac{17}{2}\)
\(=\dfrac{1}{4}-\dfrac{17}{2}=\dfrac{1}{4}-\dfrac{34}{4}=-\dfrac{33}{4}\)

a: ta có: \(\widehat{ABD}=\widehat{CBD}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACE}=\widehat{BCE}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{CBD}=\widehat{ACE}=\widehat{BCE}\)
Xét ΔABD và ΔACE có
\(\widehat{ABD}=\widehat{ACE}\)
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
=>OB=OC

Chiều dài căn phòng là:
4x1,5=6(m)
Diện tích căn phòng là 4x6=24(m2)=240000(cm2)
Diện tích 1 viên gạch men là:
30x30=900(cm2)
Số viên gạch men cần dùng là:
\(240000:900\simeq267\left(viên\right)\)

Chiều rộng công viên hình chữ nhật là :
\(1280\times\dfrac{3}{5}=768\left(m\right)\)
Diện tích công viên hình chữ nhật là :
\(1280\times768=983040\left(m^2\right)\)
Đáp số : 983040 m2

Câu 1a; giá trị chữ số 9 của số thập phân 23,987
Vì chữ số 9 của số 23,987 nằm ở hàng phần mười nên có giá trị là:
\(\dfrac{9}{10}\) = 0,9
Chọn A.0,9
b; Số lớn nhất trong các số thập phân:
23,02; 32,2; 23,2; 32,05
23,02 < 23,2 < 32,05 < 32,2
Vậy số lớn nhất trong các số đã cho là: 32,2
Chọn B. 32,2

\(\dfrac{17}{20}=\dfrac{1}{10}+\dfrac{1}{2}+\dfrac{1}{4}\)
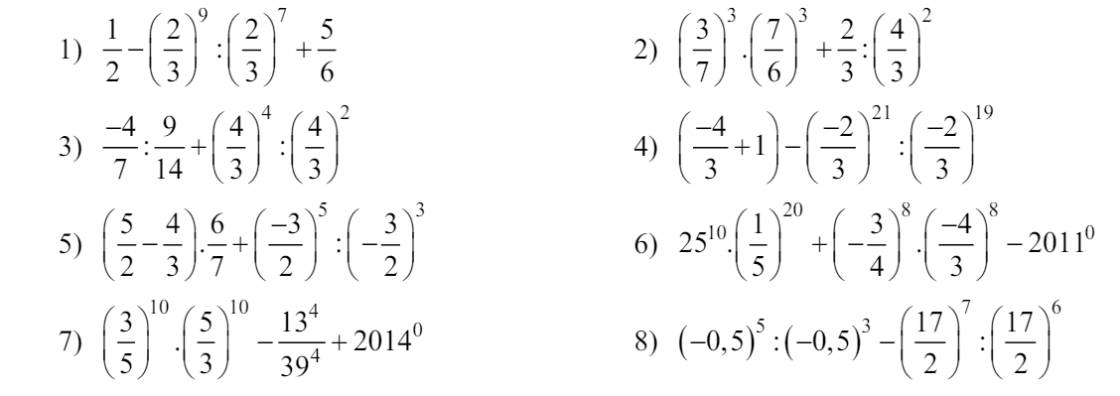


a: Xét ΔABC có
BM,CN là các đường trung tuyến
BM cắt CN tại G
Do đó: G là trọng tâm của ΔABC
=>\(GB=\dfrac{2}{3}BM;CG=\dfrac{2}{3}CN\)
mà BM=CN
nên GB=GC
b: Sửa đề: Chứng minh ΔBGN=ΔCOM
Ta có: GB+GM=BM
GC+GN=CN
mà BM=CN và GB=GC
nên GM=GN
Xét ΔGNB và ΔGMC có
GN=GM
\(\widehat{NGB}=\widehat{MGC}\)(hai góc đối đỉnh)
GB=GC
Do đó: ΔGNB=ΔGMC
c: ΔGNB=ΔGMC
=>NB=MC
mà \(NB=\dfrac{AB}{2};MC=\dfrac{AC}{2}\)
nên AB=AC
=>ΔABC cân tại A
d: Xét ΔABC có
AI,BM,CN là các đường trung tuyến
Do đó: AI,BM,CN đồng quy
vẽ hộ em bài này
4. (1,5 điểm) Cho ABC có hai đường trung tuyến BM và CN bằng nhau và cắt nhau tai G. a) Chứng minh GB = GC. b) Chứng minh BON = COM c) Chứng minh ABC cân, chỉ rõ cân tại đâu. d) Gọi I là trung điểm BC. Chứng minh AI, BM, CN đồng quy.