Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

Có \(y'=x^2-2mx-1\)
Xét pt \(y'=x^2-2mx-1=0\)(*), có \(\Delta'=m^2+1>0\) nên (*) luôn có 2 nghiệm phân biệt \(x_1,x_2\)
Theo định lý Viète, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-1\end{matrix}\right.\)
Để \(x_1^2+x_2^2=2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=2\)
\(\Leftrightarrow\left(2m\right)^2+2=2\)
\(\Leftrightarrow4m^2=0\)
\(\Leftrightarrow m=0\)
Vậy \(m=0\) thỏa mãn ycbt.

a, A''Có đúng 2 nữ''
\(C^2_3.C_{56}^2\)
\(P\left(A\right)=\dfrac{C_3^2.C_{56}^2}{C_{59}^4}\)
b, B''Có ít nhất 2 nam''
TH1 : Có 2 nam \(C_{56}^2.C_3^2\)
TH2 : Có 3 nam \(C_{56}^3.C_3^1\)
TH3 : Có 4 nam \(C^4_{56}\)
\(\Rightarrow C_{56}^2.C_3^2+C_{56}^3.C_3^1+C_{56}^4\)
\(P\left(B\right)=\dfrac{C_{56}^2.C_3^2+C_{56}^3.C_3^1+C_{56}^4}{C_{59}^4}\)
c, C''Có nhiều nhất 2 nam''
TH1 : Có 1 nam \(C_{56}^1.C_3^3\)
TH2 : Có 2 nam \(C_{56}^2.C_3^2\)
\(\Rightarrow C_{56}^2.C_3^3+C_{56}^2.C_3^2\)
\(P\left(C\right)=\dfrac{C_{56}^2.C_3^3+C^2_{56}.C_3^2}{C_{59}^4}\)

Lấy điểm A bất kì nằm trên đường tròn đáy.
Khi đó góc tạo bởi đường sinh và mặt phẳng đáy chính là \(\widehat{SAO}=45^o\)
Do đó \(h=r=\dfrac{a}{\sqrt{2}}\)
\(\Rightarrow S_{xq}=\pi rl=\pi.\dfrac{a}{\sqrt{2}}.a=\dfrac{\pi a^2}{\sqrt{2}}\)
\(S_{tp}=S_{xq}+\pi r^2=\dfrac{\pi a^2}{\sqrt{2}}+\pi\left(\dfrac{a}{\sqrt{2}}\right)^2=\dfrac{\pi a^2\sqrt{2}+\pi a^2}{2}\)

1) TXĐ: \(D=ℝ\)
\(9^x+3.6^x=4^{x+1}\)
\(\Leftrightarrow9^x-4.4^x+3.6^x=0\)
\(\Leftrightarrow\dfrac{9^x}{4^x}-4+3.\dfrac{6^x}{4^x}=0\)
\(\Leftrightarrow\left(\dfrac{9}{4}\right)^x+3\left(\dfrac{6}{4}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^2\right]^x+3\left(\dfrac{3}{2}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^x\right]^2+3\left(\dfrac{3}{2}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^x-1\right]\left[\left(\dfrac{3}{2}\right)^x+4\right]=0\)
\(\Leftrightarrow\left(\dfrac{3}{2}\right)^x=1\) (vì \(\left(\dfrac{3}{2}\right)^x>0\))
\(\Leftrightarrow x=0\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{0\right\}\)
2)
a) \(D=ℝ\)
Với \(m=1\) thì (1) thành:
\(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\sqrt{2-\sqrt{3}}\right)^{\left|x\right|}=4\)
Để ý rằng \(\sqrt{2+\sqrt{3}}.\sqrt{2-\sqrt{3}}=1\) \(\Leftrightarrow\sqrt{2-\sqrt{3}}=\dfrac{1}{\sqrt{2+\sqrt{3}}}\)
Do đó pt \(\Leftrightarrow\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\dfrac{1}{\sqrt{2+\sqrt{3}}}\right)^{\left|x\right|}-4=0\)
Đặt \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\left(t\ge1\right)\) thì pt thành:
\(t+\dfrac{1}{t}-4=0\)
\(\Leftrightarrow t^2-4t+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2+\sqrt{3}\left(nhận\right)\\t=2-\sqrt{3}\left(loại\right)\end{matrix}\right.\)
Vậy \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=2+\sqrt{3}\)
\(\Leftrightarrow\left|x\right|=2\)
\(\Leftrightarrow x=\pm2\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{\pm2\right\}\)]
2b) Đặt \(f\left(x\right)=\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\sqrt{2-\sqrt{3}}\right)^{\left|x\right|}\)
\(f\left(x\right)=\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\dfrac{1}{\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}}\)
Đặt \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\left(t\ge1\right)\) thì \(f\left(x\right)=g\left(t\right)=t+\dfrac{1}{t}\)
\(g'\left(t\right)=1-\dfrac{1}{t^2}\ge0,\forall t\ge1\)
Lập BBT, ta thấy để \(g\left(t\right)=4m\) có nghiệm thì \(t\ge1\). Tuy nhiên, với \(t>1\) thì sẽ có 2 số \(x\) thỏa mãn \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\) (là \(\log_{\sqrt{2+\sqrt{3}}}t\)
và \(-\log_{\sqrt{2+\sqrt{3}}}t\))
Với \(t=1\), chỉ có \(x=0\) là thỏa mãn. Như vậy, để pt đã cho có nghiệm duy nhất thì \(t=1\)
\(\Leftrightarrow m=g\left(1\right)=2\)
Vậy \(m=2\)
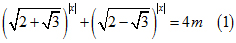 với m là tham số.
với m là tham số.
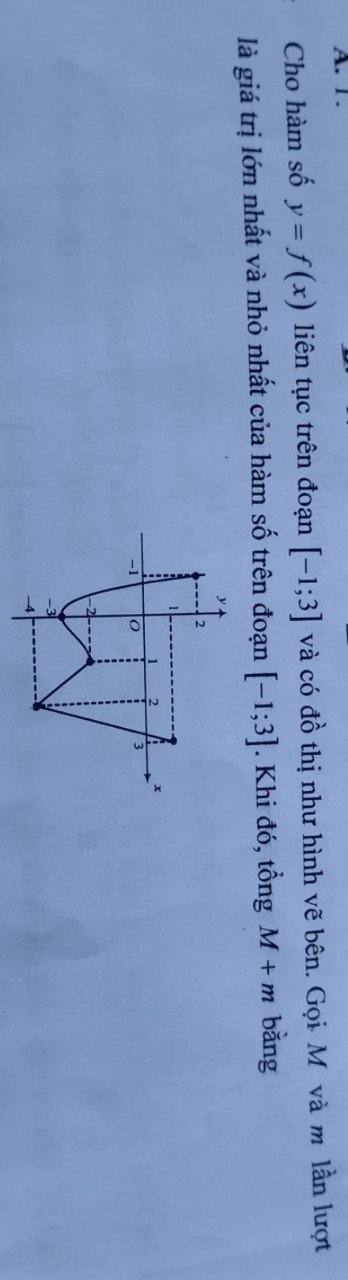
Dựa vào đồ thị, ta thấy \(m=\min\limits_{\left[-1;3\right]}f\left(x\right)=f\left(2\right)=-4\)
và \(M=\max\limits_{\left[-1;3\right]}f\left(x\right)=f\left(-1\right)=2\)
Khi đó \(M+m=2-4=-2\)