giải thích vì sao khi rewrite câu này lại sử dụng là has finished( mà không phải là finished hay finishes).
S Sharon will finish her exams. Then she will have more free time.
=> Once Sharon has finished her exams, she will have more free time.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cuộc cách mạng tư sản đã mang lại những bài học quan trọng cho nhân loại. Chúng đã đánh đổ chế độ phong kiến và giải phóng cho nhân dân, tạo điều kiện cho sự phân chia công bằng đất đai và thiết lập quyền bình đẳng giữa mọi người. Cuộc cách mạng Pháp là một ví dụ điển hình, khi nó đã lật đổ chế độ phong kiến ở Pháp và trở thành một khuôn mẫu cho các cuộc cách mạng dân chủ sau này. Cuộc cách mạng này đã đặt nền tảng cho sự phát triển của chủ nghĩa tư bản và mang lại những giá trị tự do, bình đẳng và bác ái.


| Đặc điểm khác nhau | Pha sáng | Pha tối |
| Vị trí và điều kiện xảy ra | - Diễn ra trong túi tilacoit. - Phải có ánh sáng. | - Chất nền (strôma) của lục lạp. - Phải có nguyên liệu và sản phẩm của pha sáng. |
| Nguyên liệu và năng lượng | - Năng lượng ánh sáng mặt trời, \(O_2\), \(H_2O\) - Năng lượng \(ATP\) , ánh sáng. | - \(CO_2,ATP,NADPH\) - Năng lượng \(ATP\) |
| Sản phẩm tạo ra | \(-ATP,NADPH,O_2\) | \(-Cacbonhidrat\) |
| Vai trò trong chuyển hóa năng lượng | - Chuyển đổi năng lượng ánh sáng đã được hấp thụ bởi các tế bào lục. | - Cung cấp nguyên liệu đầu vào \(ADP\) và \(NADPH\) cho pha sáng. |
| Đặc điểm khác nhau | Pha sáng | Pha tối |
| Vị trí và điều kiện xảy ra |
- Diễn ra trong túi tilacoit. - Phải có ánh sáng. |
- Chất nền (strôma) của lục lạp. - Phải có nguyên liệu và sản phẩm của pha sáng. |
| Nguyên liệu và năng lượng |
- Năng lượng ánh sáng mặt trời, �2O2, �2�H2O - Năng lượng ���ATP , ánh sáng. |
- ��2,���,�����CO2,ATP,NADPH - Năng lượng ���ATP |
| Sản phẩm tạo ra | −���,�����,�2−ATP,NADPH,O2 | −������ℎ�����−Cacbonhidrat |
| Vai trò trong chuyển hóa năng lượng | - Chuyển đổi năng lượng ánh sáng đã được hấp thụ bởi các tế bào lục. | - Cung cấp nguyên liệu đầu vào ���ADP và �����NADPH cho pha sáng. |

a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
Mà 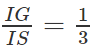
(G là trọng tâm của ∆SAB) nên
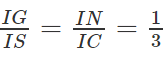
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
Ta có:

S A B C D M N O G K H P Q
a/
Ta có
\(S\in\left(SAC\right);S\in\left(SBD\right)\)
Trong mp (ABCD) gọi O là giao của AC và BD
\(O\in AC\Rightarrow O\in\left(SAC\right);O\in BD\Rightarrow O\in\left(SBD\right)\)
\(\Rightarrow SO\in\left(SAC\right)\) và \(SO\in\left(SBD\right)\) => SO là giao tuyến của (SAC) và (SBD)
b/
Trong mp (ABCD) Từ G dựng đường thẳng // AC cắt BC tại K
Xét tg SAC có
SM=AM (gt); SN=CN (gt) => MN là đường trung bình của tg SAC
=> MN//AC
Mà GM//AC
=> MN//GK mà \(G\in\left(GMN\right)\Rightarrow GK\in\left(GMN\right)\) (Từ 1 điểm trong mặt phẳng chỉ dựng được duy nhất 1 đường thẳng thuộc mặt phẳng đó và // với 1 đường thẳng cho trươc thuộc mặt phẳng)
\(\Rightarrow K\in\left(GMN\right);K\in BC\) => K llaf giao của BC với (GMN)
c/
Ta có
\(KN\in\left(GMN\right);KN\in\left(SBC\right)\) => KN là giao tuyến của (GMN) với (SBC)
Trong (ABCD) KG cắt AB tại H
\(KG\in\left(GMN\right)\Rightarrow KH\in\left(GMN\right)\)
\(KG\in\left(ABCD\right)\Rightarrow KH\in\left(ABCD\right)\)
=> KH là giao tuyến của (GMN) với (ABCD)
Ta có
\(HM\in\left(SAB\right);HM\in\left(GMN\right)\) => HM là giao tuyến của (GMN) với (SAB)
Trong mp(SAC) gọi P là giao của SO với MN
\(P\in MN\Rightarrow P\in\left(GMN\right)\)
Trong mp(SBD) Nối G với P cắt SD tại Q
\(\Rightarrow GP\in\left(GMN\right)\Rightarrow Q\in GMN\)
\(\Rightarrow MQ\in\left(GMN\right)\) mà \(MQ\in\left(SAD\right)\) => MQ là giao tuyến của (GMN) với (SAD)
Ta có
\(NQ\in\left(GMN\right);NQ\in\left(SCD\right)\) => NQ là giao tuyến của (GMN) với (SCD)
=> thiết diện của hình chóp bị cắt bởi (GMN) là đa giác HMQNK

A B C D M N E O K
Ta có
\(E\in MN\) mà \(MN\in\left(OMN\right)\Rightarrow E\in\left(OMN\right)\)
\(O\in\left(OMN\right)\)
\(\Rightarrow EO\in\left(OMN\right)\)
Ta có
\(E\in BD\) mà \(BD\in\left(BCD\right)\Rightarrow E\in\left(BCD\right)\)
\(O\in\left(BCD\right)\)
\(EO\in\left(BCD\right)\)
Trong (BCD) kéo dài EO cắt CD tại K
=> \(K\in\left(OMN\right);K\in CD\) => K chính là giao của CD với (OMN)
Câu này mình có thể sử dụng finishes cũng được
nhưng trong câu này đang muốn nhấn mạnh việc hoàn thiện này là ngay trong tương lai, nên mình sẽ dùng thì hiện tại hoàn thành nhé