#include <bits/stdc++.h>

using namespace std;

int main(){

    int n;

    cin >> n;

    long S=1;T=0;

    for (int i=1;i<=n;i++)

        if (i%2==0){

           T=T+i;

           S=S*i;

         }

    cout <<"Tong la: " <<T << endl;

    cout <<"Tich la: " <<S;

    return 0;

}

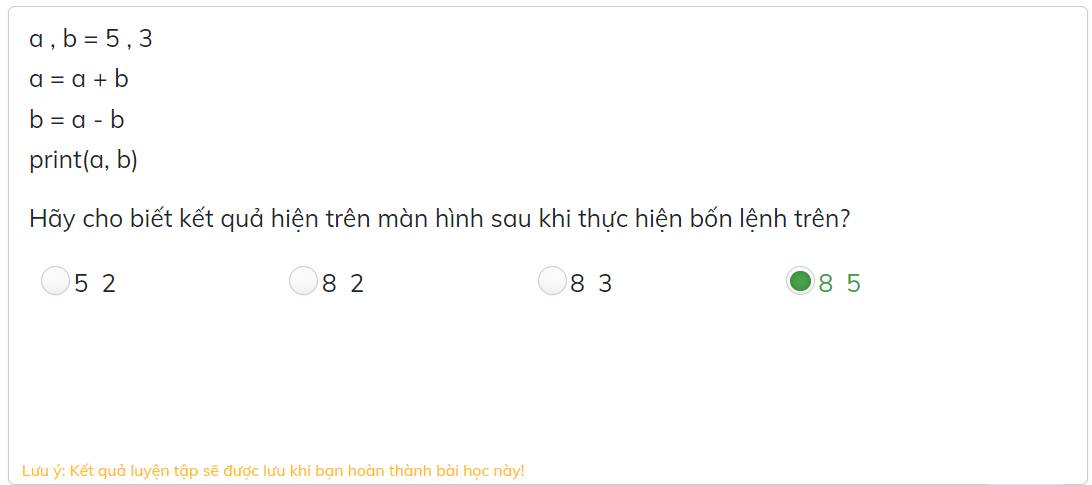
Ban đầu biến a = 5 và b = 3.

Sau khi thực hiện câu lệnh a = a + b thì a = 5 + 3 = 8

và câu lệnh tiếp là b = a - b = 8 - 3 = 5

Nên sau khi thực hiện đoạn lệnh thì a nhận giá trị là 8 và b là 5 bạn nhé

a) Từ đồ thị, ta thấy \(A\left(0;4\right),B\left(3;0\right),C\left(0;-4\right),D\left(-3;0\right)\)

b) Ta thấy O đồng thời là trung điểm của AC và II' nên AICI' là hình bình hành \(\Rightarrow\) AI' // CI hay AI' // BC (do B, I, C thẳng hàng)

 Tương tự, ta chứng minh được DI' // BC. Do đó A, I', D thẳng hàng theo tiên đề Euclide.

Lời giải:

Để 2 vecto cùng phương thì:

$\frac{m^2+m+2}{m}=\frac{4}{2}=2$ ($m\neq 0$)

$\Leftrightarrow m^2+m+2=2m$

$\Leftrightarrow m^2-m+2=0$

$\Leftrightarrow (m-0,5)^2=\frac{-7}{4}<0$ (vô lý)

Do đó không tồn tại $m$ thỏa mãn yêu cầu.

a.

Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-5;-1\right)\\\overrightarrow{DC}=\left(3-x;-2-y\right)\end{matrix}\right.\)

Do ABCD là hình bình hành \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)

\(\Rightarrow\left\{{}\begin{matrix}3-x=-5\\-2-y=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=8\\y=-1\end{matrix}\right.\)

\(\Rightarrow D\left(8;-1\right)\)

Gọi O là tâm hình bình hành \(\Rightarrow\) O là trung điểm AC

Theo công thúc trung điểm:

\(\left\{{}\begin{matrix}x_O=\dfrac{x_A+x_C}{2}=\dfrac{7}{2}\\y_O=\dfrac{y_A+y_C}{2}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow O\left(\dfrac{7}{2};\dfrac{1}{2}\right)\)

b.

Theo công thức trọng tâm: \(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=2\\y_G=\dfrac{y_A+y_B+y_C}{3}=1\end{matrix}\right.\)

\(\Rightarrow G\left(2;1\right)\)

I đối xứng B qua G \(\Rightarrow G\)  là trung điểm IB

\(\Rightarrow\left\{{}\begin{matrix}x_I=2x_G-x_B=5\\y_I=2y_G-y_B=0\end{matrix}\right.\) \(\Rightarrow I\left(5;0\right)\)

\(\left\{{}\begin{matrix}\dfrac{x_A+x_D+x_C}{3}=5=x_I\\\dfrac{y_A+y_D+y_C}{3}=0=y_I\end{matrix}\right.\) \(\Rightarrow I\) là trọng tâm ADC

c.

Ta có: \(S_{ABC}=\dfrac{1}{2}AB.d\left(C;AB\right)\)

\(S_{ABM}=\dfrac{1}{2}AB.d\left(M;AB\right)\)

\(S_{ABC}=3S_{ABM}\Rightarrow d\left(C;AB\right)=3d\left(M;AB\right)\)

\(\Rightarrow BM=\dfrac{1}{3}BC\)

\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{BM}=\dfrac{1}{3}\overrightarrow{BC}\\\overrightarrow{BM}=-\dfrac{1}{3}\overrightarrow{BC}\end{matrix}\right.\)

Gọi \(M\left(x;y\right)\Rightarrow\overrightarrow{BM}=\left(x+1;y-2\right)\)

\(\Rightarrow\left[{}\begin{matrix}\left(x+1;y-2\right)=\dfrac{1}{3}\left(4;-4\right)\\\left(x+1;y-2\right)=-\dfrac{1}{3}\left(4;-4\right)\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}\left(x;y\right)=\left(\dfrac{1}{3};\dfrac{2}{3}\right)\\\left(x;y\right)=\left(-\dfrac{7}{3};\dfrac{10}{3}\right)\end{matrix}\right.\)

Do D nằm trên trục hoành nên tọa độ có dạng \(D\left(x;0\right)\)

\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{BC}=\left(2;-2\right)\\\overrightarrow{AD}=\left(x-5;-5\right)\end{matrix}\right.\)

Do BC, AD là 2 đáy hình thang \(\Rightarrow BC||AD\)

\(\Rightarrow\overrightarrow{AD}\) cùng phương \(\overrightarrow{BC}\)

\(\Rightarrow\dfrac{x-5}{2}=\dfrac{-5}{-2}\)

\(\Rightarrow x-5=5\Rightarrow x=10\)

\(\Rightarrow D\left(10;0\right)\)

a.

\(A\left(2;-3\right)\)

Do I là trung điểm AC \(\Rightarrow\left\{{}\begin{matrix}x_C=2x_I-x_A=0\\y_C=2y_I-y_A=5\end{matrix}\right.\) 

\(\Rightarrow C\left(0;5\right)\)

\(\overrightarrow{AK}=\left(-3;5\right)\Rightarrow\) đường thẳng AB nhận \(\left(5;3\right)\) là 1 vtpt

Phương trình AB:

\(5\left(x+1\right)+3\left(y-2\right)=0\Leftrightarrow5x+3y-1=0\)

Do điểm D có hoành độ gấp đôi tung độ, gọi tọa độ D có dạng \(D\left(2d;d\right)\)

 I là tâm hình bình hành nên I là trung điểm BD

\(\Rightarrow\left\{{}\begin{matrix}x_B=2x_I-x_D=2-2d\\y_B=2y_I-y_D=2-d\end{matrix}\right.\)

B thuộc đường thẳng AB nên thay tọa độ B vào pt AB ta được:

\(5\left(2-2d\right)+3\left(2-d\right)-1=0\)

\(\Rightarrow d=\dfrac{15}{13}\Rightarrow D\left(\dfrac{30}{13};\dfrac{15}{13}\right)\)

\(\Rightarrow B\left(-\dfrac{4}{13};\dfrac{11}{13}\right)\)

b.

Gọi A' là điểm đối xứng A qua Oy \(\Rightarrow A'\left(-2;-3\right)\)

\(\Rightarrow\overrightarrow{A'D}=\left(\dfrac{56}{13};\dfrac{54}{13}\right)=\dfrac{2}{13}\left(28;27\right)\)

Đường thẳng A'D nhận \(\left(27;-28\right)\) là 1 vtpt

Phương trình A'D:

\(27\left(x+2\right)-28\left(y+3\right)=0\Leftrightarrow27x-28y-30=0\)

Gọi M' là giao điểm của A'D với Oy 

\(\Rightarrow M'\left(0;-\dfrac{15}{14}\right)\)

Do A' đối xứng A qua Oy nên: \(MA=MA'\)

\(\Rightarrow MA+MD=MA'+MD\ge A'D\)

Dấu "=" xảy ra khi và chỉ khi M, A', D thẳng hàng

Hay M là giao điểm của A'D và Oy

\(\Rightarrow M\) trùng M'

\(\Rightarrow M\left(0;-\dfrac{15}{14}\right)\)