Cho DABC. Gọi H là trực tâm của tam giác. Dựng hình bình hành BHCD. Gọi I là giao điểm của HD và BC.
a) Chứng minh 4 điểm A, B, D, C cùng thuộc một đường tròn tâm O
b) CH cắt OD tại E. Chứng minh: AB.AE = AH.AC
c) Gọi giao điểm của AI và OH là G. Chứng minh: G là trọng tâm của DABC.

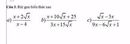
 Giải giúp bài 3 a đi
Giải giúp bài 3 a đi