
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


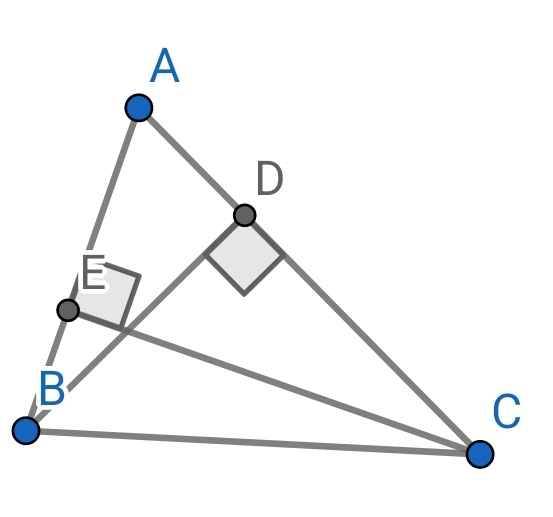
a: a: Xét ΔABC và ΔAED có
\(\dfrac{AB}{AE}=\dfrac{AC}{AD}\left(\dfrac{15}{5}=\dfrac{21}{7}=3\right)\)
\(\widehat{BAC}\) chung
Do đó: ΔABC~ΔAED
Vì \(\dfrac{AB}{AE}=\dfrac{AC}{AD}\)
nên \(AB\cdot AD=AE\cdot AC\)
b: \(\dfrac{AB}{AE}=\dfrac{AC}{AD}\)
=>\(\dfrac{AB}{AC}=\dfrac{AE}{AD}\)
Xét ΔABE và ΔACD có
\(\dfrac{AB}{AC}=\dfrac{AE}{AD}\)
\(\widehat{BAE}\) chung
Do đó: ΔABE~ΔACD
=>\(\widehat{ABE}=\widehat{ACD};\widehat{AEB}=\widehat{ADC}\)
c: Xét ΔOBD và ΔOCE có
\(\widehat{OBD}=\widehat{OCE}\)
\(\widehat{BOD}=\widehat{COE}\)(hai góc đối đỉnh)
Do đó: ΔOBD~ΔOCE
=>\(\dfrac{OB}{OC}=\dfrac{OD}{OE}\)
=>\(OB\cdot OE=OD\cdot OC\)

a: Thay x=2/3 vào A, ta được:
\(A=\dfrac{\dfrac{2}{3}-2}{\dfrac{2}{3}}=\dfrac{-4}{3}:\dfrac{2}{3}=-\dfrac{4}{3}\cdot\dfrac{3}{2}=-2\)
b: \(B=\dfrac{4x}{x+1}+\dfrac{x}{1-x}+\dfrac{2}{x^2-1}\)
\(=\dfrac{4x}{x+1}-\dfrac{x}{x-1}+\dfrac{2}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{4x\left(x-1\right)-x\left(x+1\right)+2}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{4x^2-4x-x^2-x+2}{\left(x-1\right)\left(x+1\right)}=\dfrac{3x^2-5x+2}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{\left(x-1\right)\left(3x-2\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{3x-2}{x+1}\)

a: Xét ΔMBA vuông tại M và ΔABC vuông tại A có
\(\widehat{MBA}\) chung
Do đó: ΔMBA~ΔABC
b: ΔMBA~ΔABC
=>\(\dfrac{MB}{AB}=\dfrac{BA}{BC}\left(1\right)\)
ΔBAC vuông tại A
=>\(BC^2=BA^2+AC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
ΔMBA~ΔABC
=>\(\dfrac{MA}{AC}=\dfrac{BA}{BC}\)
=>\(MA=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\)
c: Xét ΔBAM có BN là phân giác
nên \(\dfrac{BM}{BA}=\dfrac{MN}{NA}\left(2\right)\)
Xét ΔBAC có BG là phân giác
nên \(\dfrac{BA}{BC}=\dfrac{AG}{GC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{MN}{NA}=\dfrac{AG}{GC}\)
=>\(MN\cdot GC=AG\cdot NA\)

a: Xét ΔFHB vuông tại F và ΔEHC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)
Do đó: ΔFHB~ΔEHC
b: ΔFHB~ΔEHC
=>\(\dfrac{HF}{HE}=\dfrac{HB}{HC}\)
=>\(\dfrac{HF}{HB}=\dfrac{HE}{HC}\)
Xét ΔHFE và ΔHBC có
\(\dfrac{HF}{HB}=\dfrac{HE}{HC}\)
\(\widehat{FHE}=\widehat{BHC}\)(hai góc đối đỉnh)
Do đó: ΔHFE~ΔHBC
c: Sửa đề; EH là phân giác của góc FED
Xét tứ giác HECD có \(\widehat{HEC}+\widehat{HDC}=90^0+90^0=180^0\)
nên HECD là tứ giác nội tiếp
=>\(\widehat{HED}=\widehat{HCD}\)
mà \(\widehat{HCD}=\widehat{HEF}\)(ΔHCB~ΔHEF)
nên \(\widehat{HED}=\widehat{HEF}\)
=>EH là phân giác cùa góc DEF

Xét hai tam giác vuông: ∆ABD và ∆ACE có:
A chung
⇒ ∆ABD ∽ ∆ACE (g-g)
⇒ AB/AC = AD/AE
⇒ AD = AB/AC . AE
= 4/6 . 3
= 2 (cm)

Cách học tốt tất cả các loại toán, áp dụng cho tất cả các lớp:
+ Năm vững kiến thức cơ bản.
+ Thực hành, luyện tập thường xuyên để nhuần nhuyễn các kiến thức đã học, để kiến thức đã học không bị lãng quên và mai một.
+ Đọc thật kĩ đề bài. Phân tích đề bài xem đề bài đã cho gì, yêu cầu tính cái gì. Muốn tính cái đó thì cần công thức nào. Kết hợp với đề bài (những yếu tố đã cho)để tìm ra phương pháp giải
+ Làm thật chuẩn thứ tự các bước, các quy tắc, các công thức toán học
+ Đọc các loại sách tham khảo, sách nâng cao để tu dưỡng rèn luyện thêm kiến thức và kĩ năng làm toán
+ Không ngững nỗ lực tìm tòi, sáng tạo, đổi mới cách học cách làm
Trên đây là toàn bộ kĩ năng dạy toán, học toán, làm toán của cô , cô chia sẻ lại các em vận dụng sao cho phù hợp với bản thân.
Chúc các em thành công! Và sẽ sớm trở thành giáo viên toán của Olm.



a: \(3x\left(x-2\right)=x^2-4\)
=>\(3x\left(x-2\right)-\left(x-2\right)\left(x+2\right)=0\)
=>\(\left(x-2\right)\left(3x-x-2\right)=0\)
=>(x-2)(2x-2)=0
=>2(x-2)(x-1)=0
=>(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
b:
ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(\dfrac{x+3}{x-1}+\dfrac{x}{x+1}=\dfrac{x^2+4x+5}{x^2-1}\)
=>\(\dfrac{\left(x+3\right)\left(x+1\right)+x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+4x+5}{\left(x-1\right)\left(x+1\right)}\)
=>\(\left(x+3\right)\left(x+1\right)+x\left(x-1\right)=x^2+4x+5\)
=>\(x^2+4x+3+x^2-x-x^2-4x-5=0\)
=>\(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
c: \(3\left(x-1\right)< 5\left(x+1\right)-2\)
=>\(3x-3< 5x+5-2\)
=>3x-3<5x+3
=>-2x<6
=>x>-3
d: \(x^3>-2x\)
=>\(x^3+2x>0\)
=>\(x\left(x^2+2\right)>0\)
mà \(x^2+2>0\forall x\)
nên x>0