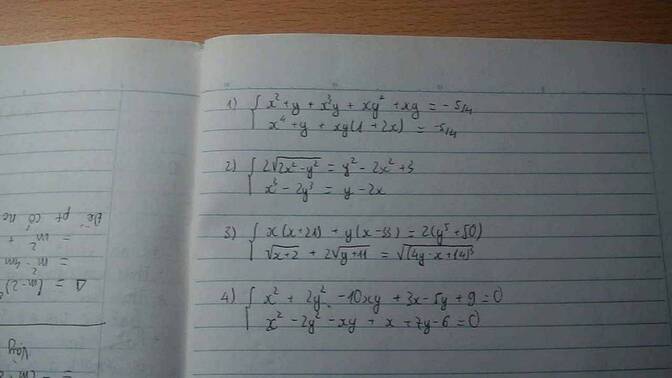
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`Answer:`
Không hiểu sao mình thấy đề thiếu ấy, định đưa về HĐT `(x^2+y)^2` nhưng mà đề chỉ có là `y`, mình nghĩ là `y^2` chứ nhỉ?
\(\hept{\begin{cases}2\sqrt{2x^2-y^2}=y^2-2x^2+3\left(1\right)\\x^3-2y^3=y-2x\left(2\right)\end{cases}}\left(ĐK:2x^2-y^2\ge0\right)\)
\(\left(1\right)\Leftrightarrow2\sqrt{2x^2-y^2}=-\left(\sqrt{2x^2-y^2}\right)^2+3\)
\(\Leftrightarrow\left(\sqrt{2x^2-y^2}\right)^2+2\sqrt{2x^2-y^2}-3=0\)
\(\Leftrightarrow\left(\sqrt{2x^2-y^2}-1\right)\left(\sqrt{2x^2-y^2}+3\right)=0\)
Vì `\sqrt{2x^2-y^2}+3>=3>0`
`<=>\sqrt{2x^2-y^2}=1`
`<=>2x^2-y^2=1(4)`
`(2)<=>x^3-2y^3=(y-2x)(2x^2-y^2)`
`<=>x^3-2y^3=2x^2y-y^3-4x^3+2xy^2`
`<=>5x^3-2x^2y-2xy^2-y^3=0(3)`
Có hệ phương trình \(\hept{\begin{cases}2x^2-y^2=1\\5x^3-2x^2y-2xy^2-y^3=0\end{cases}}\left(5\right)\)
Dễ thấy `y=0` không phải nghiệm của hệ phương trình `(5)`
Xét `y\ne0`
\(\left(3\right)\Leftrightarrow5\frac{x^3}{y^3}-\frac{2x^2}{y^2}-\frac{2x}{y}-1=0\)
\(\Leftrightarrow5\left(\frac{x}{y}\right)^3-2\left(\frac{x}{y}\right)^2-2\frac{x}{y}-1=0\)
Đặt \(a=\frac{x}{y}\)
`<=>5a^3-3a^2-2a-1=0`
`<=>5a^3-5a^2+3a^2-3a+a-1=0`
`<=>5a^2.(a-1)+3a(a-1)+(a-1)=0`
`<=>(a-1)(5a^2+3a+1)=0`
Vì `5a^2+3a+1>0`
`<=>a=1`
`<=>x=y`
`(4)<=>2x^2-x^2=1`
`<=>x^2=`
`<=>x=+-1`
Với `x=1<=>y=1`
Với `x=-1<=>y=-1`
Vậy hệ phương trình có nghiệm `(x;y)=(1;1),(-1;-1)`


Ta đổi chiều bất đẳng thức, khi đó bất đẳng thức cần chứng minh tương đương với:
\(18\left(\frac{a^3}{1+a^3}+\frac{b^3}{1+b^3}+\frac{c^3}{1+c^3}\right)+\left(a+b+c\right)^3\ge54\)
Để ý abc=1 thì \(\frac{a^3}{1+a^3}=\frac{a^3}{abc+a^3}=\frac{a^2}{bc+a^2}\)nên bất đẳng thức trên thành:
\(18\left(\frac{a^2}{bc+a^2}+\frac{b^2}{ca+b^2}+\frac{c^2}{ab+c^2}\right)+\left(a+b+c\right)^3\ge54\)
Lại cũng từ \(abc=1\) ta có \(\left(a+b+c\right)^3\ge27abc=27\), do đó ta sẽ chứng minh được khi ta chỉ ra được:
\(\frac{a^2}{bc+a^2}+\frac{b^2}{ca+b^2}+\frac{c^2}{ab+c^2}\ge\frac{3}{2}\)
Vế trái của đánh giá trên áp dụng bất đẳng thức Bunhiacopxki dạng phân thức. Lúc này ta được:
\(\frac{a^2}{bc+a^2}+\frac{b^2}{ca+b^2}+\frac{c^2}{ab+c^2}\ge\frac{\left(a+b+c\right)^2}{a^2+b^2+c^2+ab+bc+ca}\)
Tuy nhiên để đến khi \(a=b=c=1\) thì:
\(\frac{18\left(a+b+c\right)^2}{a^2+b^2+c^2+ab+bc+ca}=\left(a+b+c\right)^3=27\)
Ta sử dụng bất đẳng thức Cauchy dạng \(x+y\ge2\sqrt{xy}\), khi đó ta được:
\(\frac{18\left(a+b+c\right)^2}{a^2+b^2+c^2+ab+bc+ca}+\left(a+b+c\right)^3\ge\sqrt{\frac{18\left(a+b+c\right)^5}{a^2+b^2+c^2+ab+bc+ca}}\)
Chứng minh sẽ hoàn tất nếu ta chỉ được:
\(\sqrt{\frac{18\left(a+b+c\right)^5}{a^2+b^2+c^2+ab+bc+ca}}\ge54\Leftrightarrow\left(a+b+c\right)^5\ge\frac{81}{2}\left(a^2+b^2+c^2+ab+bc+ca\right)\)
Vậy theo bất đẳng thức Cauchy ta được:
\(\left(a+b+c\right)^6=\left[\left(a^2+b^2+c^2\right)+\left(ab+bc+ca\right)+\left(ab+bc+ca\right)\right]^3\)
\(\ge27\left(a+b+c\right)^2\left(ab+bc+ca\right)^2\ge81abc\left(a^2+b^2+c^2\right)\left(a+b+c\right)\)
\(=81\left(a^2+b^2+c^2\right)\left(a+b+c\right)\)
Khi đó ta được:
\(\left(a+b+c\right)^5\ge81\left(a^2+b^2+c^2\right)\)
Vậy ta cần chỉ ra rằng:
\(2\left(a^2+b^2+c^2\right)\ge a^2+b^2+c^2+ab+bc+ca\)
Vậy bất đẳng thức trên tương đương với \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\), là một bất đẳng thức hiển nhiên đúng.
Vậy bất đẳng thức được chứng minh, dấu đẳng thức xảy ra khi \(a=b=c=1\)

tham khảo nha
TL
a) Ta có: AM=MC=AC2AM=MC=AC2(M là trung điểm của AC)
AN=NB=AB2AN=NB=AB2(N là trung điểm của AB)
mà AC=AB(gt)
nên AM=MC=AN=NB
Xét ΔAMB và ΔANC có
AM=AN(cmt)

Ta có:
\(a+b+\sqrt{2\left(a+c\right)}=a+b+\sqrt{\frac{a+c}{2}}+\sqrt{\frac{a+c}{2}}\ge3\sqrt[3]{\frac{\left(a+b\right)\left(a+c\right)}{2}}\)
Hoàn toàn tương tự ta có:
\(\frac{1}{\left(b+c+\sqrt{2\left(b+a\right)}\right)^3}\le\frac{2}{27\left(b+c\right)\left(b+a\right)}\);
\(\frac{1}{\left(c+b+\sqrt{\left(c+b\right)}\right)^3}\le\frac{2}{27\left(c+a\right)\left(c+b\right)}\)
Cộng theo bất đẳng thức trên ta được:
\(\frac{1}{\left(a+b+\sqrt{2\left(a+c\right)}\right)^3}+\frac{1}{\left(b+c+\sqrt{2\left(b+a\right)}\right)^3}+\frac{1}{\left(c+a+\sqrt{2\left(c+b\right)}\right)^3}\)
\(\le\frac{4\left(a+b+c\right)}{27\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
Do đó:
\(\frac{1}{\left(a+b+\sqrt{2\left(a+c\right)}\right)^3}+\frac{1}{\left(b+c+\sqrt{2\left(b+a\right)}\right)^3}+\frac{1}{\left(c+a+\sqrt{2\left(c+b\right)}\right)^3}\)
\(\le\frac{1}{6\left(ab+bc+ca\right)}\)
Vậy bất đẳng thức được chứng minh, bất đẳng thức xày ra khi \(a=b=c=\frac{1}{4}\)

Từ bất đẳng thức Cô si ta có:
\(4\left(ab+bc+ca\right)\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\le\left[\frac{ab+bc+ca}{ca}+ca\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\right]^2\)
\(\Rightarrow\)Ta cần chứng minh:
\(\frac{ab+bc+ca}{ca}+ca\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\le\frac{a+b}{c}+\frac{b+c}{a}+\frac{c+a}{b}\)
Vì vai trò của a, b, c trong bất đẳng thức như nhau, nên không mất tính tổng quát ta giả sử \(a\ge b\ge c\)nên bất đẳng thức cuối cùng đùng. Vậy bất đẳng thức được chứng minh.

Ta viết lại bất đẳng thức trên thành:
\(\frac{a-b}{b}-\frac{a-b}{c}+\frac{c-a}{a}-\frac{c-a}{c}\ge\frac{\left(a-c\right)^2}{\left(a+b\right)\left(b+c\right)}\)
Hay: \(\frac{\left(a-b\right)\left(c-b\right)}{bc}+\frac{\left(c-a\right)^2}{ca}\ge\frac{\left(a-c\right)^2}{\left(a+b\right)\left(b+c\right)}\)
Tiếp tục khai triển và thu gọn ta được:
\(\Leftrightarrow b\left(c-a\right)^2\left(b^2+ab+bc\right)\ge a\left(a-b\right)\left(b-c\right)\left(a+b\right)\left(b+c\right)\)
\(\Leftrightarrow\left(b-ac\right)^2\ge0\)
Bất đẳng thức cuối cùng luôn đúng hay bài toán được chứng minh xong.

`Answer:`
ĐK: `x^3-1>=0`
`<=>(x-1)(x^2+x+1)>0`
`<=>x>=1`
PT tương đương: `2.(x^2+x+1)+3(x-1)=7\sqrt{(x^2+x+1)(x-1)}`
Đặt `a=\sqrt{x^2+x+1}<=>a^2=x^2+x+1;b=\sqrt{x-1}<=>b^2=x-1`
PT tương đương: `2a^2+3b^2=7ab`
`<=>2a^2-7ab+3b^2=0`
`<=>2a^2-ab-6ab+3b^2=0`
`<=>a(2a-b)-3b(2a-1)=0`
`<=>(2a-b)(a-3b)=0`
`<=>2a=b` hoặc `a=3b`
Với `2a=b:`
`2\sqrt{x^2+x+1}=3\sqrt{x-1}`
`<=>4(x^2+x+1)=9(x-1)`
`<=>4x^2-5x+13=0`
`\Delta=5^2-4.4.13<0`
Vậy phương trình vô nghiệm.
Với `a=3b:`
`\sqrt{x^2+x+1}=3\sqrt{x-1}`
`<=>x^2+x+1=9(x-1)`
`<=>x^2-8x+10=0`
`\Delta'=4^2-10=6`
`<=>x=4+-\sqrt{6}`
Vậy phương trình cố nghiệm là `x=4+-\sqrt{6}`
`

+) Tìm trên mạng thì đề thiếu xy + yz - zx = 7
+) Nếu bổ sung đề: Tìm x; y ; z nguyên dương thì có thể làm như sau:
Không mất tính tổng quát: g/s:
x ≥ y ≥ z
Vì x2 + y2 + z2 = 14 =>
x 2 ≤ 14
⇒ x ≤ √ 14 < 4
Vì x nguyên dương
=> x ∈ { 1; 2; 3}
+)Vớix=3=>\hept{y+z=3y2+z2=5⇒\hept{y+z=y2≤5
