Gọi d=ƯCLN(2n+1;3n+2)

=>\(\left\{{}\begin{matrix}2n+1⋮d\\3n+2⋮d\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}6n+3⋮d\\6n+4⋮d\end{matrix}\right.\)

=>\(6n+4-6n-3⋮d\)

=>\(1⋮d\)

=>d=1

=>ƯCLN(2n+1;3n+2)=1

=>\(\dfrac{2n+1}{3n+2}\) là phân số tối giản

- Năng lượng gió có thể làm cây bị cong hoặc gãy. Năng lượng gió càng lớn thì lực tác dụng lên cây càng mạnh, cây càng dễ bị đổ.

- Năng lượng gió có thể làm quay chong chóng. Năng lượng gió càng lớn thì lực tác dụng lên chong chóng càng mạnh, chong chóng quay càng nhanh. 

Năng lượng có đặc trưng cho khả năng tác dụng lực.

Ví dụ:

- Khi một quả bóng được ném lên cao: Năng lượng cơ học của quả bóng chuyển từ dạng động năng (khi di chuyển) sang dạng thế năng hấp dẫn (khi ở độ cao nhất).

- Khi lò xo được nén: Năng lượng cơ học của lò xo chuyển từ dạng động năng (khi nén) sang dạng thế năng đàn hồi (khi được nén).

- Khi nước chảy từ trên cao xuống: Năng lượng thế năng hấp dẫn của nước chuyển sang dạng động năng (khi nước chảy).

Đặt \(B=4^{2023}+4^{2022}+...+4^2+5\)

=>\(B=4^{2023}+4^{2022}+...+4^2+4+1\) và \(A=75B+25\)

\(B=4^{2023}+4^{2022}+...+4^2+4+1\)

=>\(4B=4^{2024}+4^{2023}+...+4^3+4^2+4\)

=>\(4B-B=4^{2024}+4^{2023}+...+4^3+4^2+4-4^{2023}-4^{2022}-...-4^2-4-1\)

=>\(3B=4^{2024}-1\)

=>\(B=\dfrac{4^{2024}-1}{3}\)

\(A=75\cdot B+25=75\cdot\dfrac{4^{2024}-1}{3}+25\)

\(=25\left(4^{2024}-1\right)+25\)

\(=25\cdot4^{2024}⋮4^{2024}\)

Open the window; it's absolutely boiling in here.

\(3\cdot5^{x-1}+6250=25^3\)

=>\(\dfrac{3}{5}\cdot5^x=25^3-6250=9375\)

=>\(5^x=9375:\dfrac{3}{5}=15625\)

=>x=6

a: Vì O nằm trên đoạn AB

nên O nằm giữa A và B

=>OA+OB=AB

=>OA+2=7

=>OA=5(cm)

b: I nằm trên đoạn AO

=>I nằm giữa A và O

=>AI+IO=AO

=>IO+3=5

=>IO=2(cm)

Vì OA và OB là hai tia đối nhau

nên OI và OB là hai tia đối nhau

=>O nằm giữa I và B

mà OI=OB(=2cm)

nên O là trung điểm của BI

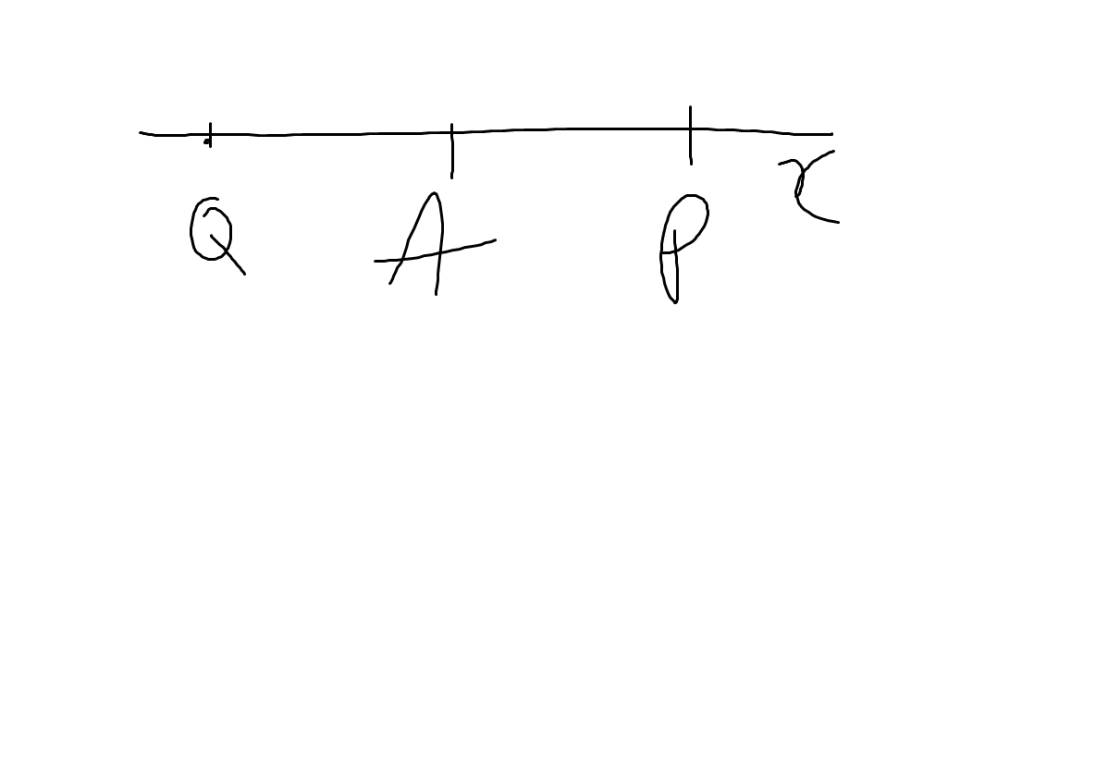
Vì AP và AQ là hai tia đối nhau

nên A nằm giữa P và Q

\(A=\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{98\cdot99}+\dfrac{1}{99\cdot100}\)

\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)

\(=\dfrac{1}{2}-\dfrac{1}{100}=\dfrac{49}{100}\)

Hãy viết phân số 7/12 dưới dạng tổng của hai phân số có tử số là 1 mẫu số khác nhau

a: Số bài đạt điểm trung bình là \(60\cdot25\%=15\left(bài\right)\)

Số bài còn lại là 60-15=45(bài)

Số bài đạt điểm khá là \(45\cdot\dfrac{1}{3}=15\left(bài\right)\)

Số bài đạt điểm giỏi là 45-15=30(bài)

b: Tỉ số phần trăm giữa số bài đạt điểm khá và đạt điểm trung bình là:

15:15=100%

\(\dfrac{1}{1\cdot6}+\dfrac{1}{6\cdot11}+...+\dfrac{1}{496\cdot501}\)

\(=\dfrac{1}{5}\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{496\cdot501}\right)\)

\(=\dfrac{1}{5}\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{496}-\dfrac{1}{501}\right)\)

\(=\dfrac{1}{5}\left(1-\dfrac{1}{501}\right)=\dfrac{1}{5}\cdot\dfrac{500}{501}=\dfrac{100}{501}\)

\(B=\dfrac{1}{1.6}+\dfrac{1}{6.11}+\dfrac{1}{11.16}+...+\dfrac{1}{496.501}\)
\(\Rightarrow5B=\dfrac{5}{1.6}+\dfrac{5}{6.11}+\dfrac{5}{11.16}+...+\dfrac{5}{496.501}\)
\(\Rightarrow5B=\dfrac{6-1}{1.6}+\dfrac{11-6}{6.11}+\dfrac{16-11}{11.16}+...+\dfrac{501-496}{496.501}\)
\(\Rightarrow5B=\dfrac{1}{1}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}+...+\dfrac{1}{496}-\dfrac{1}{501}\)
\(\Rightarrow5B=\dfrac{1}{1}-\dfrac{1}{501}\)
\(\Rightarrow5B=\dfrac{500}{501}\)
\(\Rightarrow B=\dfrac{100}{501}\)