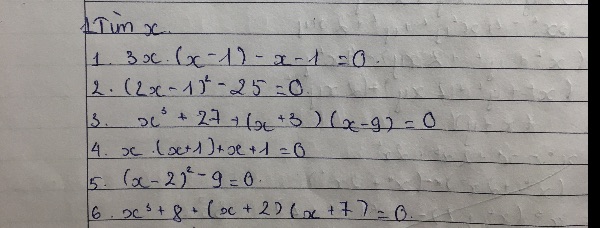Cho hình bình hành ABCD có tâm đối xứng là O, E là điểm bất kỳ trên đoạn OD. Gọi F là điểm đối xứng của C qua E. Tứ giác ODFA là hình gì?

A. Hình thang                                              B. Hình bình hành

C. Hình thang cân                                      D. Hình thang vuông

 tứ giác ODFA là hình bình hành 

HOK TỐT

\(2m^2+10m+8\)

\(=2\left(m^2+5m+4\right)\)

\(=2\left(m^2+4m+m+4\right)\)

\(=2\left(m+4\right)\left(m+1\right)\)

=2m²+8m+2m+8

=(2m²+2m)+(8m+8)

=2m(m+1)+8(m+1)

=(m+1)(2m+8)

=(m+1)2(m+4)

=2(m+1)(m+4)

HT~

\(\left(x-3\right)^3+\left(3-x\right)=0\)

\(=\left(x-3\right)^3-\left(x-3\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(x-4\right)\left(x-2\right)=0\)

\(\Leftrightarrow x=2,3,4\)

\(a^2-b^2-c^2+2bc\)

\(=a^2-\left(b-c\right)^2\)

\(=\left(a-b+c\right)\left(a+b-c\right)\)

r sao nữa hả bạn

2)

\(\left(2x-1\right)^2-25=0\)

\(\Leftrightarrow\left(2x-1\right)^2=25\)

\(\Leftrightarrow\orbr{\begin{cases}2x-1=5\\2x-1=-5\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-2\end{cases}}\)

4)

\(x\left(x+1\right)+x+1=0\)

\(\Leftrightarrow\left(x+1\right)^2=0\)

\(\Leftrightarrow x=-1\)

\(f\left(x\right)=2x^3+3x^2-10x+a\)

\(f\left(x\right)\)chia hết cho \(x-2\)nên \(f\left(x\right)=\left(x-2\right).q\left(x\right)\)(\(q\left(x\right)\)là đa thức thương) 

suy ra \(f\left(2\right)=0\)

\(\Rightarrow2.2^3+3.2^2-10.2+a=0\)

\(\Leftrightarrow a=-8\)

Áp dụng định lý Bezout

\(f\left(2\right)=2.2^3+3.2^2-10.2+a=8+a\)

Mà để cho \(2x^3+3x^2-10x+a⋮x-2\)

\(\Rightarrow f\left(2\right)=0\)

\(\Rightarrow8+a=0\)

\(\Rightarrow a=-8\)

Vậy \(a=-8\) để \(2x^3+3x^2-10x+a⋮x-2\)

\(5xy.\left(3x^2-xy+4\right)\)

\(=5xy.3x^2-5xy.xy+5xy.4\)

\(=15x^3y-5x^2y+20xy\)

Vì hình thang \(ABCD\)cân có đáy \(AB\)nên \(\widehat{D}=\widehat{C}=80^o\)

\(\widehat{B}+\widehat{C}=180^o\Leftrightarrow\widehat{B}=180^o-\widehat{C}=180^o=80^o=100^o\)

em cảm ơn