Gía trị lớn nhất của x thỏa mãn x3 - 19x- 30= 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) A = x^2 + 3x + 10
=x^2 + 2x.3/2 + 9/4 + 31/4
=(x+3/2)^2 + 31/4
mà (x+ 3/2 )^2 >=0 với mọi x
=> Min (x+3/2)^2 = 0
=> Min (x+3/2)^2 + 31/4 = 31/4
Vậy GTNN của A là 31/4 khi:
x+ 3/2 = 0 <=> x= - 3/2



a) \(A=2x^2-10x+2021=2\left(x^2-5x+\frac{25}{4}\right)+\frac{4017}{2}\)
\(=2\left(x-\frac{5}{2}\right)^2+\frac{4017}{2}\ge\frac{4017}{2}\)
Dấu \(=\)khi \(x-\frac{5}{2}=0\Leftrightarrow x=\frac{5}{2}\)
b) \(B=x^2-7x-2008=x^2-7x+\frac{49}{4}-\frac{8081}{4}=\left(x-\frac{7}{2}\right)^2-\frac{8081}{4}\ge-\frac{8081}{4}\)
Dấu \(=\)khi \(x-\frac{7}{2}=0\Leftrightarrow x=\frac{7}{2}\)
c) \(C=2021-10x-x^2=-\left(x^2+10x+25\right)+2046=-\left(x+5\right)^2+2046\le2046\)
Dấu \(=\)khi \(x+5=0\Leftrightarrow x=-5\).
d) \(D=2008+10x-2x^2=-2\left(x^2-5x+\frac{25}{4}\right)+\frac{4041}{2}=-2\left(x-\frac{5}{2}\right)^2+\frac{4041}{2}\le\frac{4041}{2}\)
Dấu \(=\)khi \(x-\frac{5}{2}=0\Leftrightarrow x=\frac{5}{2}\).

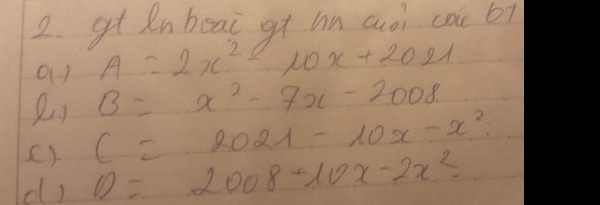
\(x^3-19x-30=0\)
\(\Rightarrow x^3-25x+6x-30=0\)
\(\Rightarrow x\left(x^2-25\right)+6\left(x-5\right)=0\)
\(\Rightarrow x\left(x^2-5^2\right)+6\left(x-5\right)=0\)
\(\Rightarrow x\left(x-5\right)\left(x+5\right)+6\left(x-5\right)=0\)
\(\Rightarrow\left(x-5\right)[x\left(x+5\right)+6]=0\)
\(\Rightarrow\left(x-5\right)\left(x^2+5x+6\right)=0\)
\(\Rightarrow\left(x-5\right)\left(x^2+2x+3x+6\right)=0\)
\(\Rightarrow\left(x-5\right)[x\left(x+2\right)+3\left(x+2\right)]=0\)
\(\Rightarrow\left(x+2\right)\left(x+3\right)\left(x-5\right)=0\)
Trường hợp 1: \(x+2=0\Rightarrow x=-2\)
Trường hợp 2: \(x+3=0\Rightarrow x=-3\)
Trường hợp 3: \(x-5=0\Rightarrow x=5\)
Vậy giá trị lớn nhất của \(x=5\)
\(x^3-19x-30=0\)
\(\Leftrightarrow x^3-5x^2+5x^2-25x+6x-30=0\)
\(\Leftrightarrow\left(x-5\right)\left(x^2+5x+6\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x^2+3x+2x+6\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+3\right)\left(x+2\right)=0\)
\(\Leftrightarrow x-5=0\)hoặc \(x+3=0\)hoặc \(x+2=0\)
\(\Leftrightarrow x=5\)hoặc \(x=-3\)hoặc \(x=-2\).
Vậy \(x=5\)là giá trị thỏa mãn ycbt.