 giải giúp em với ạ em cần gấp, em cảm ơn trước ạ
giải giúp em với ạ em cần gấp, em cảm ơn trước ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


= khi phương trình có 2 vế là 1 đẳng thức hoặc bất đẳng thức => khi phương trình có 1 vế là 1 biểu thức (tham khảo)


a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
nên MAOB là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{MAD}\) là góc tạo bởi tiếp tuyến AM và dây cung AD
\(\widehat{ACD}\) là góc nội tiếp chắn cung AD
Do đó: \(\widehat{MAD}=\widehat{ACD}\)
Xét ΔMAD và ΔMCA có
\(\widehat{MAD}=\widehat{MCA}\)
\(\widehat{AMD}\) chung
Do đó: ΔMAD~ΔMCA
=>\(\dfrac{MA}{MC}=\dfrac{MD}{MA}\)
=>\(MA^2=MD\cdot MC\)

a: Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
DO đó: ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
b: TA có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
=>AM\(\perp\)DE
Ta có: ΔADE cân tại A
mà AM là đường cao
nên AM là phân giác của góc DAE
c: Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{BDH}=\widehat{CEK}\)(ΔABD=ΔACE)
Do đó: ΔHBD=ΔKCE
=>BH=CK
d: Gọi O là giao điểm của BH với CK
Ta có: \(\widehat{OBC}=\widehat{HBD}\)(hai góc đối đỉnh)
\(\widehat{OCB}=\widehat{KCE}\)(hai góc đối đỉnh)
mà \(\widehat{HBD}=\widehat{KCE}\)(ΔHBD=ΔKCE)
nên \(\widehat{OBC}=\widehat{OCB}\)
=>OB=OC
=>O nằm trên đường trung trực của BC(1)
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC(2)
Từ (1),(2) suy ra A,M,O thẳng hàng
=>AM,BH,CK đồng quy

a) Hàm số đồng biến khi x > 0 (do a = 3 > 0)
b) Hàm số nghịch biến khi x < 0 (do a = 3 > 0)
c) Bảng giá trị:
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(y=3x^2\) | \(12\) | \(3\) | \(0\) | \(3\) | \(12\) |
Đồ thị:

1: Thay x=36 vào A, ta được:
\(A=\dfrac{36-5}{\sqrt{36}}=\dfrac{31}{6}\)
2: \(B=\dfrac{2x+\sqrt{x}}{x-1}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\dfrac{2x+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\dfrac{2x+\sqrt{x}+\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
3: \(P=A\cdot B=\dfrac{3x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{x-5}{\sqrt{x}}\)
\(=\dfrac{\left(x-5\right)\left(3\sqrt{x}+2\right)}{x-1}=\dfrac{\left(x-1\right)\left(3\sqrt{x}+2\right)-4\left(3\sqrt{x}+2\right)}{x-1}\)
\(=3\sqrt{x}+2-\dfrac{4\left(3\sqrt{x}+2\right)}{x-1}\)
Để P là số nguyên thì \(3\sqrt{x}+2⋮x-1\)
=>\(\left(3\sqrt{x}+2\right)\left(3\sqrt{x}-2\right)⋮x-1\)
=>\(9x-4⋮x-1\)
=>\(9x-9+5⋮x-1\)
=>\(5⋮x-1\)
=>\(x-1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{2;0;6;-4\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{2;6\right\}\)
Khi x=2 thì \(P=3\sqrt{2}+2-\dfrac{4\left(3\sqrt{2}+2\right)}{2-1}\)
\(=3\sqrt{2}+2-4\left(3\sqrt{2}+2\right)=-3\left(3\sqrt{2}+2\right)\notin Z\)
=>Loại
Khi x=6 thì \(P=3\sqrt{6}+2-\dfrac{4\left(3\sqrt{6}+2\right)}{6-1}=3\sqrt{6}+2-\dfrac{4}{5}\left(3\sqrt{6}+2\right)\)
\(=\dfrac{1}{5}\left(3\sqrt{6}+2\right)\notin Z\)
=>Loại
Vậy: \(x\in\varnothing\)

\(1\ge\dfrac{1}{a+1}+\dfrac{1}{b+1}+\dfrac{1}{c+1}\ge\dfrac{9}{a+1+b+1+c+1}\)
\(\Rightarrow a+b+c+3\ge9\Rightarrow a+b+c\ge6\)
Ta có:
\(\dfrac{a^3}{a^2+ab+b^2}=\dfrac{a\left(a^2+ab+b^2\right)-a\left(ab+b^2\right)}{a^2+ab+b^2}\)
\(=a-\dfrac{ab\left(a+b\right)}{a^2+ab+b^2}\ge a-\dfrac{ab\left(a+b\right)}{3\sqrt[3]{a^2.ab.b^2}}=a-\dfrac{a+b}{3}=\dfrac{2a}{3}-\dfrac{b}{3}\)
Tương tự: \(\dfrac{b^3}{b^2+bc+c^2}\ge\dfrac{2b}{3}-\dfrac{c}{3}\)
\(\dfrac{c^3}{c^2+ca+a^2}\ge\dfrac{2c}{3}-\dfrac{a}{3}\)
Cộng vế:
\(\dfrac{a^3}{a^2+ab+b^2}+\dfrac{b^3}{b^2+bc+c^2}+\dfrac{c^3}{c^2+ca+a^2}\ge\dfrac{a+b+c}{3}\ge\dfrac{6}{3}=2\)
Dấu "=" xảy ra khi \(a=b=c=2\)

ĐKXĐ: \(x\ne0;y\ne0\)
y-x=6
=>y=x+6
\(\dfrac{12}{x}-\dfrac{12}{y}=\dfrac{1}{10}\)
=>\(\dfrac{12}{x}-\dfrac{12}{x+6}=\dfrac{1}{10}\)
=>\(\dfrac{12\left(x+6\right)-12x}{x\left(x+6\right)}=\dfrac{1}{10}\)
=>\(\dfrac{72}{x\left(x+6\right)}=\dfrac{1}{10}\)
=>\(x\left(x+6\right)=720\)
=>\(x^2+6x-720=0\)
=>\(x^2+6x+9=729\)
=>\(\left(x+3\right)^2=729\)
=>\(\left[{}\begin{matrix}x+3=27\\x+3=-27\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=24\left(nhận\right)\\x=-30\left(nhận\right)\end{matrix}\right.\)
Khi x=24 thì \(y=x+6=24+6=30\left(nhận\right)\)
Khi x=-30 thì \(y=x+6=-30+6=-24\left(nhận\right)\)

Để A là số nguyên dương thì \(\left\{{}\begin{matrix}\sqrt{x}⋮\sqrt{x}+3\\A>0\end{matrix}\right.\)
=>\(\sqrt{x}+3-3⋮\sqrt{x}+3\)
=>\(-3⋮\sqrt{x}+3\)
=>\(\sqrt{x}+3\in\left\{1;-1;3;-3\right\}\)
=>\(\sqrt{x}+3=3\)
=>x=0(loại)
vậy: Không có giá trị nào của x để A là số nguyên dương


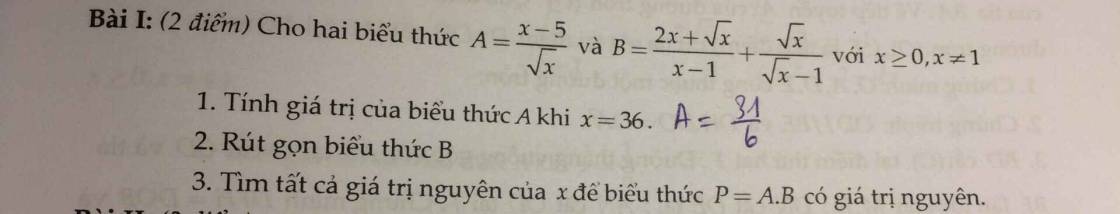

a.
Phương trình có nghiệm khi:
\(\Delta'=\left(m+1\right)^2+7m^2\ge0\)
\(\Leftrightarrow8m^2+2m+1\ge0\)
\(\Leftrightarrow8\left(m+\dfrac{1}{8}\right)^2+\dfrac{7}{8}>0\) (luôn đúng)
Vậy pt luôn có nghiệm với mọi m
b.
Pt có nghiệm kép khi:
\(\Delta=\left(m+1\right)^2-48=0\)
\(\Leftrightarrow m^2+2m-47=0\)
\(\Rightarrow m=-1\pm4\sqrt{3}\)
c.
Pt có nghiệm \(x=-3\) khi:
\(2.\left(-3\right)^2-m^2.\left(-3\right)+18m=0\)
\(\Leftrightarrow3m^2+18m+18=0\Rightarrow m=-3\pm\sqrt{3}\)
a: \(\text{Δ}=\left[-2\left(m+1\right)\right]^2-4\cdot7\cdot\left(-m^2\right)\)
\(=4\left(m^2+2m+1\right)+28m^2\)
\(=32m^2+8m+4\)
\(=32\left(m^2+\dfrac{1}{4}m+\dfrac{1}{8}\right)\)
\(=32\left(m^2+2\cdot m\cdot\dfrac{1}{8}+\dfrac{1}{64}+\dfrac{7}{64}\right)\)
\(=32\left(m+\dfrac{1}{8}\right)^2+\dfrac{7}{2}>=\dfrac{7}{2}>0\forall m\)
=>Phương trình luôn có nghiệm
b: \(\text{Δ}=\left(m+1\right)^2-4\cdot3\cdot4=\left(m+1\right)^2-48\)
Để phương trình có nghiệm kép thì Δ=0
=>\(\left(m+1\right)^2-48=0\)
=>\(\left(m+1\right)^2=48\)
=>\(m+1=\pm4\sqrt{3}\)
=>\(m=\pm4\sqrt{3}-1\)
c: Thay x=-3 vào phương trình, ta được:
\(2\cdot\left(-3\right)^2-m^2\cdot\left(-3\right)+18\cdot m=0\)
=>\(3m^2+18m+18=0\)
=>\(m^2+6m+6=0\)
=>\(\left(m+3\right)^2=3\)
=>\(m+3=\pm\sqrt{3}\)
=>\(m=\pm\sqrt{3}-3\)