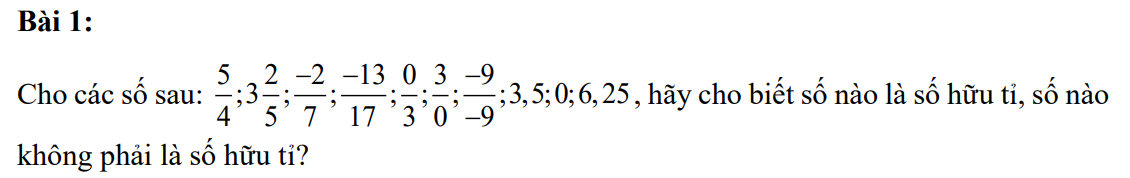
Giúp mik với, pls
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x-1}{2011}+\dfrac{x-2}{2010}+\dfrac{x-3}{2009}+\dfrac{x-4}{2008}=4\)
=>\(\left(\dfrac{x-1}{2011}-1\right)+\left(\dfrac{x-2}{2010}-1\right)+\left(\dfrac{x-3}{2009}-1\right)+\left(\dfrac{x-4}{2008}-1\right)=0\)
=>\(\dfrac{x-2012}{2011}+\dfrac{x-2012}{2010}+\dfrac{x-2012}{2009}+\dfrac{x-2012}{2008}=0\)
=>\(\left(x-2012\right)\left(\dfrac{1}{2011}+\dfrac{1}{2010}+\dfrac{1}{2009}+\dfrac{1}{2008}\right)=0\)
=>x-2012=0
=>x=2012
\(\dfrac{x-1}{2011}+\dfrac{x-2}{2010}+\dfrac{x-3}{2009}+\dfrac{x-4}{2008}=4\\ \left(\dfrac{x-1}{2011}-1\right)+\left(\dfrac{x-2}{2010}-1\right)+\left(\dfrac{x-3}{2009}-1\right)+\left(\dfrac{x-4}{2008}-1\right)=0\\ \dfrac{x-2012}{2011}+\dfrac{x-2012}{2010}+\dfrac{x-2012}{2009}+\dfrac{x-2012}{2008}=0\\ \left(x-2012\right)\left(\dfrac{1}{2011}+\dfrac{1}{2010}+\dfrac{1}{2009}+\dfrac{1}{2008}\right)=0\\ x-2012=0\\ x=2012\)

\(\left[\left(\dfrac{4}{3}\right)^{-3}\cdot\left(\dfrac{3}{4}\right)^5\right]:\left(\dfrac{3}{8}\right)^7\\ =\left[\left(\dfrac{3}{4}\right)^3\cdot\left(\dfrac{3}{4}\right)^5\right]:\left(\dfrac{3}{8}\right)^7\\ =\left(\dfrac{3}{4}\right)^{3+5}:\dfrac{3^7}{8^7}\\ =\left(\dfrac{3}{4}\right)^8\cdot\dfrac{8^7}{3^7}\\ =\dfrac{3^8}{4^8}\cdot\dfrac{8^7}{3^7}\\ =\dfrac{3^8}{2^{16}}\cdot\dfrac{2^{21}}{3^7}=3\cdot2^5=3\cdot32=96\)
\(\left[\left(\dfrac{4}{3}\right)^{-3}\cdot\left(\dfrac{3}{4}\right)^5\right]:\left(\dfrac{3}{8}\right)^7\)
\(=\left[\left(\dfrac{3}{4}\right)^3\cdot\left(\dfrac{3}{4}\right)^5\right]:\dfrac{3^7}{8^7}\)
\(=\left(\dfrac{3}{4}\right)^8\cdot\dfrac{8^7}{3^7}=\dfrac{3^8}{4^8}\cdot\dfrac{8^7}{3^7}=\dfrac{3\cdot2^{21}}{2^{16}}=3\cdot2^5=3\cdot32=96\)


a: Các cặp góc đối đỉnh là: \(\widehat{xOt};\widehat{yOz}\) và \(\widehat{xOz};\widehat{yOt}\)
b: Các cặp góc kề bù là:
\(\widehat{xOt};\widehat{xOz}\)
\(\widehat{xOt};\widehat{tOy}\)
\(\widehat{zOy};\widehat{zOx}\)
\(\widehat{zOy};\widehat{tOy}\)
c: \(\widehat{xOt}+\widehat{xOz}=180^0\)(hai góc kề bù)
=>\(\widehat{xOz}+45^0=180^0\)
=>\(\widehat{xOz}=135^0\)
Ta có: \(\widehat{xOt}=\widehat{yOz}\)(hai góc đối đỉnh)
mà \(\widehat{xOt}=45^0\)
nên \(\widehat{yOz}=45^0\)
Ta có: \(\widehat{xOz}=\widehat{yOt}\)(hai góc đối đỉnh)
mà \(\widehat{xOz}=135^0\)
nên \(\widehat{yOt}=135^0\)

Bài 3:
Ta có: \(\dfrac{1}{5^2}< \dfrac{1}{4\cdot5};\dfrac{1}{6^2}< \dfrac{1}{5\cdot6};...;\dfrac{1}{100^2}< \dfrac{1}{99\cdot100}\)
\(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+...+\dfrac{1}{99\cdot100}\\=> \dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ =>\dfrac{1}{5^2}+\dfrac{1}{6^2}+..+\dfrac{1}{100^2}< \dfrac{1}{4}-\dfrac{1}{100}< \dfrac{1}{4}\left(1\right)\)
Ta có: \(\dfrac{1}{5^2}>\dfrac{1}{5\cdot6};\dfrac{1}{6^2}>\dfrac{1}{6\cdot7};...;\dfrac{1}{100^2}>\dfrac{1}{100\cdot101}\)
\(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}>\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+..+\dfrac{1}{100\cdot101}\\ =>\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}>\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{100}-\dfrac{1}{101}\\ =>\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}>\dfrac{1}{5}-\dfrac{1}{101}=\dfrac{96}{505}>\dfrac{96}{576}=\dfrac{1}{6}\left(2\right)\)
Từ (1) và (2) => \(\dfrac{1}{6}< \dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4}\)

a) Ta có: \(\widehat{cNb}+\widehat{MNb}=180^{\circ}\) (hai góc kề bù)
\(\Rightarrow\widehat{MNb}=180^{\circ}-\widehat{cNb}=180^{\circ}-55^{\circ}=125^{\circ}\)
b) Ta có: \(\widehat{MNb}=\widehat{aMN}\left(=125^{\circ}\right)\)
Mà hai góc này đều nằm ở vị trí so le trong
Nên \(Ma//Nb\)

\(7+\left(\dfrac{7}{12}-\dfrac{1}{2}+3\right)-\left(\dfrac{1}{12}+5\right)\)
\(=7+\left(\dfrac{7}{12}-\dfrac{6}{12}+3\right)-\left(\dfrac{1}{12}+5\right)\)
\(=7+3+\dfrac{1}{12}-\dfrac{1}{12}-5\)
=10-5=5

\(-\dfrac{1}{12}-\left(-\dfrac{1}{10}\right)\\ =-\dfrac{1}{12}+\dfrac{1}{10}\\ =\dfrac{-5}{60}+\dfrac{6}{60}\\ =\dfrac{-5+6}{60}\\ =\dfrac{1}{60}\)

\(\left(7-\dfrac{1}{5}+\dfrac{1}{3}\right)-\left(6+\dfrac{9}{5}+\dfrac{4}{3}\right)\\ =7-\dfrac{1}{5}+\dfrac{1}{3}-6-\dfrac{9}{5}-\dfrac{4}{3}\\ =\left(7-6\right)-\left(\dfrac{1}{5}+\dfrac{9}{5}\right)+\left(\dfrac{1}{3}-\dfrac{4}{3}\right)\\ =1-2-1\\ =-2\)
\(\left(7-\dfrac{1}{5} +\dfrac{1}{3}\right)-\left(6+\dfrac{9}{5}+\dfrac{4}{3}\right)\)
\(=7-\dfrac{1}{5}+\dfrac{1}{3}-6-\dfrac{9}{5}-\dfrac{4}{3}\)
\(=\left(7-6\right)-\left(\dfrac{1}{5}+\dfrac{9}{5}\right)+\left(\dfrac{1}{3}-\dfrac{4}{3}\right)-\dfrac{1}{3}\)
\(=1-2+\left(-1\right)-\dfrac{1}{3}\)
\(=\left[1+\left(-1\right)\right]-2-\dfrac{1}{3}\)
\(=0-2-\dfrac{1}{3}\)
\(=-2-\dfrac{1}{3}\)
\(=-\dfrac{6}{3}-\dfrac{1}{3}\)
\(=-\dfrac{7}{3}\)
Số hữu tỉ là \(\dfrac{5}{4};3\dfrac{2}{5};\dfrac{-2}{7};\dfrac{-13}{17};\dfrac{0}{3};\dfrac{-9}{-9};3,5;0;6,25\)
Số không là số hữu tỉ là \(\dfrac{3}{0}\)