Cho tia Ox , vẽ hai tia Oy và Ot nằm cùng phía với đường thẳng chứa tia Ox sao cho: xoy = 30độ, xot = 70độ
a) Tính yot? Tia Oy có là tia phân giác của xot không? Vì sao?
b) Gọi tia Om là tia đối của tia Ox .Tính số đo của mot?
c) Gọi Oz là tia phân giác của mot. Hỏi tia Oz có vuông góc với tia Oy không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a)`Ta có: \(\left\{{}\begin{matrix}AB\perp AC\\HE\perp AC\end{matrix}\right.\) \(\Rightarrow\)`AB////HE`
`b)`Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{C}=180^o-90^o-60^o=30^o\)
Xét tam giác AHC, có:
\(\widehat{HAC}=180^o-30^o-90^o=60^o\)
\(\widehat{A}=\widehat{BAH}+\widehat{HAC}\)
\(\Rightarrow\widehat{BAH}=90^o-60^o=30^o\)
Ta có: \(\widehat{BAH}=\widehat{AHE}=30^o\) ( so le trong )

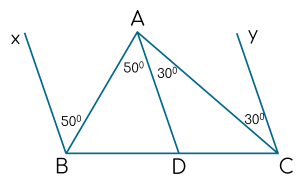
Vì \(\widehat{xBA}=\widehat{BAD}\left(=50^o\right)\) mà \(\widehat{xBA}\text{ và }\widehat{BAD}\) là 2 góc so le trong
=> Bx//AD (1)
Vì \(\widehat{DAC}=\widehat{ACy}\left(=30^o\right)\) mà \(\widehat{DAC}\text{ và }\widehat{ACy}\) là 2 góc so le trong
=> AD // Cy (2)
Từ (1) và (2) => Bx // Cy
Ta có:
`@` \(\widehat{ABx}=\widehat{DAB}=50^o\)
`=>Bx////AD` ( 2 góc so le trong bằng nhau ) (1)
`@`\(\widehat{ACy}=\widehat{DAC}=30^o\)
`=>Cy////AD` ( 2 góc so le trong bằng nhau ) (2)
\(\left(1\right);\left(2\right)\Rightarrow\)`Bx////Cy`

A B C D E F 1 2 2
Thầy ơi , đề sai ạ =))
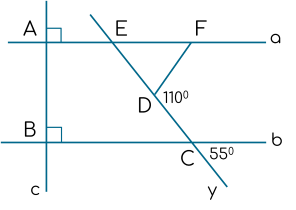
a) Vì a ⊥ c ; b ⊥ c => a // b ( từ vuông góc đên song song )
b) Vì Dn là tia phân giác của \(\widehat{FDC}\) ( giả thiết )
\(\Rightarrow\widehat{D_1}=\widehat{D_2}=\dfrac{\widehat{FDC}}{2}=\dfrac{110^o}{2}=55^o\)
Mà \(\widehat{bCy}=55^o\) \(\Rightarrow\widehat{D_2}=\widehat{bCy}\) mà \(\widehat{D_2}\text{ và }\widehat{bCy}\) là 2 góc so le trong
=> Dn // b mà b // a ( phần a )
=> Dn // a

\(\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}\)Theo tc dãy tỉ số bằng nhau ta có
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{10}{5}=2\Rightarrow x=6;y=4\)
Ta có : 2x = 3y => \(\dfrac{x}{3}=\dfrac{y}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{10}{5}=2\) ( do x + y = 10 )
\(\Rightarrow\left\{{}\begin{matrix}x=2.3=6\\y=2.2=4\end{matrix}\right.\)

\(x-\dfrac{10}{3}=\dfrac{7}{15}.\dfrac{3}{5}\Leftrightarrow x-\dfrac{10}{3}=\dfrac{7}{25}\Leftrightarrow x=\dfrac{7}{25}+\dfrac{10}{3}=\dfrac{21+250}{75}=\dfrac{271}{75}\)

\(A=\dfrac{3x+6}{3x+1}=\dfrac{3x+1+5}{3x+1}=1+\dfrac{6}{3x+1}\)
\(\Rightarrow3x+1\inƯ\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
| 3x+1 | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| x | 0 | loại | loại | -1 | loại | loại | loại | loại |
\(B=\dfrac{2x-8}{2x-1}=\dfrac{2x-7-1}{2x-1}=1-\dfrac{7}{2x-1}\Rightarrow2x-1\inƯ\left(-7\right)\left\{\pm1;\pm7\right\}\)
| 2x-1 | 1 | -1 | 7 | -7 |
| x | 1 | 0 | 4 | -3 |