Question

[Nguyễn Văn Tiến Dũng]

Một người đi xe đạp đi trên một đường thẳng. Ban đầu, người đó đi từ nhà (điểm A) đến cửa hàng (điểm B) cách nhà 4 km trong 15 phút. Sau đó, người đó quay về một hiệu sách (điểm C) nằm giữa nhà và cửa hàng, cách cửa hàng 1 km trong 5 phút.
a) Tính tốc độ trung bình trên từng chặng đường (AB và BC).
b) Tính tốc độ trung bình trên cả quãng đường đi.
c) Tính vận tốc trung bình trên cả quãng đường đi.

giải giúp mik vs ạ (cụ thể thì càng tốt nha)

Answer 1

[subjects]

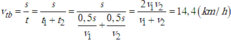
đổi: \(15p=\frac14h;5p=\frac{1}{12}h\)

a. tốc độ người đó trên chặn đường AB là:

\(v_{AB}=\frac{s_{AB}}{t_{AB}}=\frac{4}{\frac14}=16\) (km/h)

tốc độ người đó trên chặng đường BC là:

\(v_{BC}=\frac{s_{BC}}{t_{BC}}=\frac{1}{\frac{1}{12}}=12\) (km/h)

b. tốc độ người đó trên cả quãng đường đi là:

\(v_{TB}=\frac{s_{AB}+s_{BC}}{t_{AB}+t_{BC}}=\frac{4+1}{\frac14+\frac{1}{12}}=15\) (km/h)

c. vận tốc trung bình người đó trên cả quãng đường là:

\(v_{TB}^{\prime}=\frac{s_{AC}}{t_{AB}+t_{BC}}=\frac{s_{AB}-s_{BC}}{t_{AB}+t_{BC}}=\frac{4-1}{\frac14+\frac{1}{12}}=9\) (km/h)

kết luận: ...

Answer 2

[subjects]