Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ABCD là hình thang cân
=>\(\hat{ADC}=\hat{BCD}\)
mà \(\hat{ADC}=2\cdot\hat{BDC}\) (DB là phân giác của góc ADC)
nên \(\hat{BCD}=2\cdot\hat{BDC}\)
Xét ΔBDC vuông tại B có \(\hat{BDC}+\hat{BCD}=90^0\)
=>\(2\cdot\hat{BDC}+\hat{BDC}=90^0\)
=>\(3\cdot\hat{BDC}=90^0\)
=>\(\hat{BDC}=\frac{90^0}{3}=30^0\)
\(\hat{ADC}=2\cdot\hat{BDC}=2\cdot30^0=60^0\)
ABCD là hình thang cân
=>\(\hat{ADC}=\hat{BCD}\)
=>\(\hat{BCD}=60^0\)
AB//CD
=>\(\hat{BAD}+\hat{ADC}=180^0\)
=>\(\hat{BAD}=180^0-60^0=120^0\)
ABCD là hình thang cân
=>\(\hat{BAD}=\hat{ABC}\)
=>\(\hat{ABC}=120^0\)
b: Ta có: AB//CD
=>\(\hat{ABD}=\hat{BDC}\) (hai góc so le trong)
mà \(\hat{ADB}=\hat{BDC}\)
nên \(\hat{ABD}=\hat{ADB}\)
=>AB=AD
mà AD=BC(ABCD là hình thang cân)
nên AB=AD=BC=6(cm)
Xét ΔBCD vuông tại B có \(\sin CDB=\frac{CB}{CD}\)
=>\(\frac{6}{CD}=\sin30=\frac12\)
=>\(CD=2\cdot6=12\left(\operatorname{cm}\right)\)
Chu vi hình thang ABCD là:
AB+BC+CD+DA
=6+6+6+12=18+12=30(cm)
a) Các góc của hình thang đều bằng \(90^{\circ}\).
b) Khi \(B C = 6\), chu vi hình thang bằng 24 cm.

a) Xét tứ giác ABCD có:
. M là trung điểm của BC ( AM là đường trung tuyến)
. M là tđ của AD ( gt)
Vậy: ABCD là hbh ( tứ giác có 2 đường chéo cắt nhau tại tđ của mỗi đường)
mà \(\widehat{BAC}\) = 900 ( \(\Delta\) ABC vuông tại A)
--> ABCD là hình chữ nhật ( hbh có 1 góc vuông)
b) Ta có: \(IA\perp AC\)
\(CD\perp AC\)
\(\Rightarrow\) IA // CD
Xét tứ giác BIDC có:
. IA // CD (cmt)
\(\Rightarrow\) IB // CD ( B ϵ IA )
. AB =CD ( cạnh đối hcn ABCD )
mà AB = IB ( tính chất đối xứng)
\(\Rightarrow\) IB = CD ( cùng = AB )
Vậy: BIDC là hbh ( tứ giác có 2 cạnh đối vừa //, vừa = nhau)
\(\Rightarrow\) BC // ID ( cạnh đối hbh)
" đề câu c sai nha bạn"

Bài 1:
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
DO đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC
hay BEFC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BEFC là hình thang cân

Hình vẽ ;
A D B C E 60 o
a, Chứng minh tứ giác ABCD là hình thang cân .
Xét tam giác ADC ( góc ACD = 90 độ do AC\(⊥\)CD-gt) ta có :
\(\widehat{D}+\widehat{CAD}=90^o\)
\(\Rightarrow\widehat{CAD}=90^o-\widehat{D}=90^o-60^o=30^o\)
mà \(\widehat{CAD}=\widehat{BAC}\left(gt\right)\Rightarrow\widehat{BAC}=30^o\)
Ta có : \(\widehat{BAD}=\widehat{BAC}+\widehat{CAD}=30^o+30^o=60^o\)
Xét hình thang ABCD , ta có :
\(\widehat{BAD}=\widehat{D}=60^o\)
\(\Rightarrow\)tứ giác ABCD là hình thang cân.
b, Tính AD.
Kéo dài AB và DC cắt nhau tại E .
Xét tam giác AED , ta có : \(\widehat{BAC}=\widehat{CAD}\left(gt\right)\)
\(AC⊥CD\)(gt)
=> tam giác AED là tam giác cân .
mà góc D = 60 độ (gt)
=> tam giác AED là tam giác đều
=>\(\hept{\begin{cases}AB=CD=\frac{1}{2}AD\left(1\right)\\CE=CD\end{cases}}\)
Xét tam giác ADE , ta có :
BC//AD( do ABCD là hình thang )
CE=CD( cmt)
=> BC là đường trung bình của tam giác ADE
=>\(BC=\frac{1}{2}AD\left(2\right)\)
Từ (1) và (2) => BC=CD=AB=\(\frac{1}{2}.AD\)
Theo giả thiết , ta có :
AB+BC+CD+AD=20
=>\(\frac{1}{2}AD+\frac{1}{2}AD+\frac{1}{2}AD+AD=20\)
=>\(\frac{5}{2}AD=20\Rightarrow AD=8\left(cm\right)\)
Nên nhớ hình vẽ chỉ mang tính minh họa cho bài làm nên ko được đẹp lắm đâu các bạn thông cảm cho.
Trong bài mk làm hơi tắt có j hk hiểu nhắn tin hỏi mk .

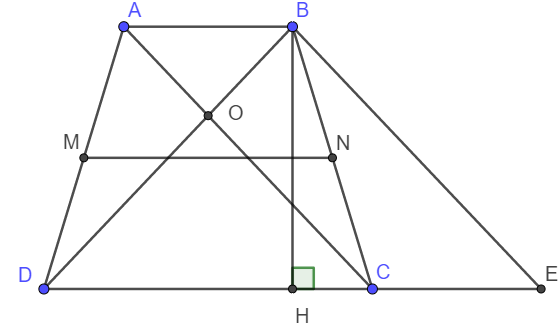
a) Xét tứ giác ABEC có AB // CE; AC // BE .
Vậy nên ABEC là hình bình hành. Suy ra AB = CE.
Do MN là đường trung bình hình thang ABCD nên ta có :
\(MN=\frac{AB+DC}{2}=\frac{CE+DC}{2}=\frac{DE}{2}.\)
b) Do ABCD là hình thang cân nên ta có:
\(AD=BC;DB=AC\)
Xét tam giác ABD và tam giác BAC có:
Cạnh AB chung
AD = BC
BD = AC
\(\Rightarrow\Delta ABD=\Delta BAC\left(c-c-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{BAC}\) hay \(\widehat{ABO}=\widehat{BAO}\)
Xét tam giác OAB có \(\widehat{ABO}=\widehat{BAO}\) nê OAB là tam giác cân tại O.
c) Do ABEC là hình bình hành nên AC = BE
Lại có AC = BD nên BD = BE
Suy ra tam giác BDE cân tại B.
Tam giác cân BDE có BH là đường cao nên đồng thời là đường trung tuyến.
Lại có theo câu a thì MN = DE/2
Giả thiết lại cho MN = BH. Vậy nên BH = DE/2
Xét tam giác BDE có trung tuyến BH bằng một nửa cạnh tướng ứng nên BDE là tam giác vuông tại B.
Vậy BDE là tam giác vuông cân tại B.

Bài 1: Giải: Xét tam giác ACD có F,G lần lượt là trung điểm AC,DC nên FG là đường trung bình
\(\Rightarrow\)\(FG//AD\)
C/m tương tự đc \(EH//AD; GH//EF//BC\)
\(\Rightarrow EFGH\) là hình bình hành
a/Để EFGH là hình chữ nhật thì góc \(FGH=90^o\)
\(\Rightarrow góc HGD+góc FGC=90^o\)
Mà góc HGD=góc BCD;góc FGC= góc ADC ( góc đồng vị = nhau)
\(\Rightarrow\) góc BCD+góc ADC=\(90^o\)
\(\Rightarrow\)Để EFGH là hình chữ nhật thì tứ giác ABCD cần có góc BCD+góc ADC=\(90^o\)
b/Để EFGH là hình thoi thì FG=HG
Mà FG=1/2AD; HG=1/2BC
\(\Rightarrow\)AD=BC
\(\Rightarrow\)Để EFGH là hình thoi thì tứ giác ABCD có AD=BC
c/ để EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật vừa là hình thoi\(\Rightarrow \)ABCD phải có đủ cả 2 điều kiện trên

- Bài 1
a) Xét tam giác BCD có BM=MD(gt), BN=NC(gt) => MN là đg` TB => MN// DC => MN// DE(1)
và MN=1/2DC => MN= DE(2)
từ (1)và (2) => MNED là hbh
b) MNED là hbh(câu a) => MD//NE => ADM= DEN(đồng vị)
Xét tam giác ABD vg tại A có BM=DM=> AM là trung tuyến => AM=1/2BD= MD
=> tam giác ADM cân tại M => MDA = DAM
=> DEN= MAD (3)
MN//DE=> MN//AE => AMNE là hình thang (4)
từ (3)và (4) => AMNE là hình thang cân
c) để MNED là hình thoi \Leftrightarrow MNED là hbh có MD=DE \Leftrightarrow 1/2BD=1/2CD \Leftrightarrow BD = CD \Leftrightarrow tam giác BCD cân tại D \Leftrightarrow DBC=góc C \Leftrightarrow góc C=1/2góc B\Leftrightarrow góc C=2góc B
Vậy để MNED là hình thoi thì tam giác ABC có góc C=2góc B17 Tháng mười hai 2013#2 
nhuquynhdatGuest
bài 2
a) AB//CD => AB//CE(1)
Xét tam giác ADE có AH là đg` cao
lại có E đối xứng với D qua H => H là trung điểm của DE => AH là trung tuyến
=> tam giác ADE cân tại A
=> ADE=AED(goác đáy tam giác cân)
mặt khác ABCD là hình thang cân => ADC=góc C
=> góc C= AED
mà 2 góc này ở vị trí đồng vị của AE và BC => AE//BC(2)
từ (1)và (2) => ABCE là hbh
b) xét tam giác AHE và tam giác FHD có góc AHE=góc DHF(đối đỉnh)
DH=HE(gt)
AE//DF(gt)=> AEH=FDH(SLT)
=>tam giác AHE=tam giác FHD(gcg) => AH=HF => H là TĐ của AF
c) Ta có AH=HF(câu b)DH=HE(gt) => ADFE là hbh
mà AH vg góc với ED=> AF vg góc với ED => ADEF là hình thoi
lại có tam giác ADE cân tại A (câu a)=> AD=AE => ADEF là hình vg
a) Xét hình thang cân ABCD, ta có: AB // CD, AC = BD (tc hbh)
Xét tứ giác ABEC, ta có: AB = EC (gt), AB // CE (cmt)
=> ABEC là hình bình hành (DHNB)
=> AC // BE (tc hbh)
Mà AC vuông góc BD tại O => DB vuông góc BE tại D
Mặt khác BE = BD (= AC) (cmt)
=> tam giác DBE vuông cân tại B (DHNB)