Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O A B x y M N *: Nhớ bổ sung thêm đường tròn tâm A,B
a) Xét \(\Delta\)OMA và \(\Delta\)OMB:
OA = OB
OM chung
AM = BM
=> \(\Delta\)OMA = \(\Delta\)OMB (c.c.c)
b) Xét \(\Delta\)ONA và \(\Delta\)ONB :
OA = OB
ON chung
AN = BN
=> \(\Delta\)ONA = \(\Delta\)ONB (c.c.c)
c) Ta có: AM = BM và M nằm trong góc xOy^ => M nằm trên tia phân giác của xOy^ (1)
và AN = BN và N nằm trong góc xOy^ => N nằm trên tia phân giác của góc xOy^ (2)
Từ (1) và (2) => O,M,N thẳng hàng
d) Xét \(\Delta\)AMN và \(\Delta\)BMN :
AM = BM
MN chung
AN = BN
=> \(\Delta\)AMN = \(\Delta\)BMN (c.c.c)
e) Ta có: AN = BN và N nằm trong AMB^
=> MN là tia phân giác của góc AMB^

) Xét
Δ
ΔOMA và
Δ
ΔOMB:
OA = OB
OM chung
AM = BM
=>
Δ
ΔOMA =
Δ
ΔOMB (c.c.c)
b) Xét
Δ
ΔONA và
Δ
ΔONB :
OA = OB
ON chung
AN = BN
=>
Δ
ΔONA =
Δ
ΔONB (c.c.c)
c) Ta có: AM = BM và M nằm trong góc xOy^ => M nằm trên tia phân giác của xOy^ (1)
và AN = BN và N nằm trong góc xOy^ => N nằm trên tia phân giác của góc xOy^ (2)
Từ (1) và (2) => O,M,N thẳng hàng
d) Xét
Δ
ΔAMN và
Δ
ΔBMN :
AM = BM
MN chung
AN = BN
=>
Δ
ΔAMN =
Δ
ΔBMN (c.c.c)
e) Ta có: AN = BN và N nằm trong AMB^
=> MN là tia phân giác của góc AMB^

a) Xét \(\Delta\)OMA và \(\Delta\)OMB có :
OM chung
OA = OB(gt)
MA = MB(vì có cùng bán kính)
=> \(\Delta\)OMA = \(\Delta\)OMB(c.c.c)
Xét \(\Delta\)ONA và \(\Delta\)ONB có :
ON chung
OA = OB(gt)
NA = NB(vì có cùng bán kính)
\(\Delta\)ONA = \(\Delta\)ONB(c.c.c)
b) Có \(\Delta\)OMA = \(\Delta\)OMB(c.c.c , theo câu a)
=> ^MOA = ^MOB
=> OM là tia phân giác của ^AOB (1)
\(\Delta\)ONA = \(\Delta\)ONB(theo câu a)
=> ^NOA = ^NOB(hai góc tương ứng)
=> ON là tia pg của ^xOy(2)
Từ (1) và (2) => O,M,N thẳng hàng
c) Xét \(\Delta\)AMN và \(\Delta\)BMN có :
AM = BM(cmt)
MN chung
AN = BN(cmt)
=> \(\Delta\)AMN = \(\Delta\)BMN(c.c.c)
=> ^MAN = ^MBN ( hai góc tương ứng)
d) Lại có : ^MAN = ^MBN(hai góc tương ứng) => MN là phân giác của ^AMB ( k phải là ^AMN)

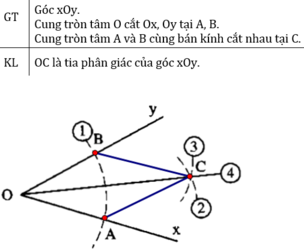
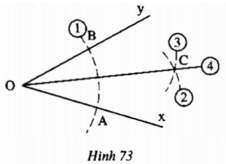
Nối BC, AC
ΔOBC và ΔOAC có:
OB = OA (bán kính)
AC = BC (gt)
OC cạnh chung
Nên ΔOBC = ΔOAC (c.c.c)
nên OC là tia phân giác của góc xOy.
Xét ΔOAB và ΔOAC:
OB = OC
AB = AC
OA chung
=> ΔOAB = ΔOAC (c.c.c)
=> ∠AOB = ∠AOC
Xét ΔOBD và ΔOCD:
OB = OC
BD = CD
OD chung
=> ΔOBD = ΔOCD (c.c.c)
=> ∠BOD = ∠COD
=> ∠AOB + ∠BOD = ∠AOC + ∠COD
=> ∠AOD = ∠AOD
=> OA và OD trùng nhau hoặc ∠AOD = 180 độ
=> O, A, D thẳng hàng.
cho mình xin tích nhé !
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(1)
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Ta có: DC=DB
=>D nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra O,A,D thẳng hàng