
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Rút gọn phân số:
a) \(-\frac{11}{43}=-\frac{11}{43}\) (phân số này tối giản rồi cần gì rút gọn nữa bạn).
b) \(\frac{17.5-17}{3-20}=\frac{68}{-17}=\frac{-68}{17}=-4.\)
c) \(\frac{3.21}{14.15}=\frac{63}{210}=\frac{3}{10}.\)
d) \(\frac{3.4+3.11}{3-13}=\frac{45}{-10}=\frac{-45}{10}=-\frac{9}{2}.\)
Chúc bạn học tốt!

a/
Theo đề,ta có:
+/ \(\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}\left(1\right)\)
+/\(\dfrac{y}{4}=\dfrac{z}{5}\Rightarrow\dfrac{y}{12}=\dfrac{z}{15}\)\(\left(2\right)\)
Từ (1) và (2), ta có:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x-y-z}{8-12-15}=\dfrac{28}{-19}\)
Do đó:
+/ \(\dfrac{x}{8}=\dfrac{28}{-19}\Rightarrow x=-\dfrac{224}{19}\)
+/\(\dfrac{y}{12}=\dfrac{28}{-19}\Rightarrow y=-\dfrac{336}{19}\)
+/\(\dfrac{z}{15}=\dfrac{28}{-19}\Rightarrow z=-\dfrac{420}{19}\)
Vậy: + \(x=-\dfrac{224}{19}\)
+ \(y=-\dfrac{336}{19}\)
+ \(z=-\dfrac{420}{19}\)
a,x2=y3,y4=z5x2=y3,y4=z5và x-y-z=28
Có \(\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}\)
\(\dfrac{y}{4}=\dfrac{z}{5}\Rightarrow\dfrac{y}{12}=\dfrac{z}{15}\)
=>\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
Áp dụng tính chất DTSBN có:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)=\(\dfrac{x-y-z}{8-12-15}=\dfrac{-28}{19}\)
=> x=\(\dfrac{-224}{19}\)
y=\(\dfrac{-336}{19}\)
z=\(\dfrac{-420}{19}\)

\(\left|x\right|=7\)
\(\Rightarrow\orbr{\begin{cases}x=7\\x=-7\end{cases}}\)
Vậy \(x\in\left\{\pm7\right\}\)

\(\Rightarrow\dfrac{1}{3}\left(x-\dfrac{3}{2}\right)+\dfrac{1}{2}\left(2x+1\right)=\dfrac{-13}{3}\)
\(\Rightarrow\dfrac{1}{3}x-\dfrac{1}{2}+x+\dfrac{1}{2}=\dfrac{-13}{3}\)
\(\Rightarrow\dfrac{4}{3}x=\dfrac{-13}{3}\Rightarrow x=\dfrac{-13}{4}\)

a) \(-6.\left(-\frac{2}{3}\right).0,25\)
\(=-6.\left(-\frac{2}{3}\right).\frac{1}{4}\)
\(=4.\frac{1}{4}\)
\(=1.\)
b) \(-\frac{15}{4}.\left(-\frac{7}{15}\right).\left(-2\frac{2}{5}\right)\)
\(=-\frac{15}{4}.\left(-\frac{7}{15}\right).\left(-\frac{12}{5}\right)\)
\(=\frac{7}{4}.\left(-\frac{12}{5}\right)\)
\(=-\frac{21}{5}.\)
c) \(\left(-0,4\right)^2-\left(-0,4\right)^3.\left(-3\right)\)
\(=0,16-\left(-0,064\right).\left(-3\right)\)
\(=0,16-0,192\)
\(=-0,032.\)
Chúc bạn học tốt!

b: \(\sqrt{8^2+6^2}-\sqrt{16}+\dfrac{1}{2}\sqrt{\dfrac{4}{25}}\)
\(=10-4+\dfrac{1}{2}\cdot\dfrac{2}{5}=6+\dfrac{1}{5}=\dfrac{31}{5}\)

\(\left(\dfrac{1}{3}\right)^{50}.\left(-9\right)^{25}-\dfrac{2}{3}:4\)
=\(\left(\dfrac{1}{9}\right)^{25}.\left(-9\right)^{25}-\dfrac{1}{6}\)
=\(\left[\dfrac{1}{9}.\left(-9\right)\right]^{25}-\dfrac{1}{6}\)
= \(\left(-1\right)^{25}-\dfrac{1}{6}\)
= \(-1-\dfrac{1}{6}=\dfrac{-7}{6}\)
\(\left(\dfrac{1}{3}\right)^{50}\cdot\left(-9\right)^{25}-\dfrac{2}{3}:4\)
\(=\left[\left(\dfrac{1}{3}\right)^2\right]^{25}\cdot\left(-9\right)^{25}-\dfrac{1}{6}\)
\(=\left(\dfrac{1}{9}\right)^{25}\cdot\left(-9\right)^{25}-\dfrac{1}{6}\)
\(=\left[\dfrac{1}{9}\cdot\left(-9\right)\right]^{25}-\dfrac{1}{6}\)
\(=\left(-1\right)^{25}-\dfrac{1}{6}=-1-\dfrac{1}{6}=-\dfrac{7}{6}\)

1) \(\left|x\right|=7\)
=> \(\left[{}\begin{matrix}x=7\\x=-7\end{matrix}\right.\)
Vậy \(x\in\left\{7;-7\right\}.\)
2) \(\left|x\right|=0\)
=> \(x=0\)
Vậy \(x\in\left\{0\right\}.\)
5) \(\left|x\right|-1=\frac{2}{5}\)
=> \(\left|x\right|=\frac{2}{5}+1\)
=> \(\left|x\right|=\frac{7}{5}\)
=> \(\left[{}\begin{matrix}x=\frac{7}{5}\\x=-\frac{7}{5}\end{matrix}\right.\)
Vậy \(x\in\left\{\frac{7}{5};-\frac{7}{5}\right\}.\)
8) \(\left|x-17\right|=23\)
=> \(\left[{}\begin{matrix}x-17=23\\x-17=-23\end{matrix}\right.\) => \(\left[{}\begin{matrix}x=23+17\\x=\left(-23\right)+17\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x=40\\x=-6\end{matrix}\right.\)
Vậy \(x\in\left\{40;-6\right\}.\)
Mình chỉ làm thế thôi nhé, bạn đăng hơi nhiều mà với cả mấy câu này dễ mà bạn.
Chúc bạn học tốt!
1) |x|=7
=> [x=7x=−7 =>[x=7x=−7
Vậy x∈{7;−7}.x∈{7;−7}.
2) |x|=0
=> x=0x=0
Vậy x∈{0}.x∈{0}.
5) |x|−1=25
=> |x|=25+1 =>|x|=25+1
=> |x|=75|x|=75
=> [x=75x=−75[x=75x=−75
Vậy x∈{75;−75}.x∈{75;−75}.
8) |x−17|=23
=> [x−17=23x−17=−23[x−17=23x−17=−23 => [x=23+17x=(−23)+17[x=23+17x=(−23)+17
=> [x=40x=−6[x=40x=−6
Vậy x∈{40;−6}.
mình làm tới đây thôi dài quá:)
tick cho mình nha

a) Vì |x - 3,5| ≥ 0∀x
|4,5 - y| ≥ 0∀y
=> |x - 3,5| + |4,5 - y| ≥ 0 ∀x,y
Dấu " = " xảy ra khi và chỉ khi |x - 3,5| = 0 hoặc |4,5 - y| = 0 => x = 3,5 hoặc y = 4,5
Vậy GTNN = 0 khi x = 3,5;y = 4,5
b) |x - 2| ≥ 0 ∀x
|3 - y| ≥ 0 ∀y
=> |x - 2| + |3 - y| ≥ 0 ∀x,y
Dấu " = " xảy ra khi và chỉ khi \(\left\{{}\begin{matrix}x-2=0\\3-y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
Vậy GTNN = 0 <=> x = 2,y = 3
c) \(\left|x+\frac{2}{3}\right|+\left|y-\frac{3}{4}\right|+\left|z-5\right|=0\)
Vì \(\left\{{}\begin{matrix}\left|x+\frac{2}{3}\right|\ge0\forall x\\\left|y-\frac{3}{4}\right|\ge0\forall y\\\left|z-5\right|\ge0\forall z\end{matrix}\right.\)
=> \(\left|x+\frac{2}{3}\right|+\left|y-\frac{3}{4}\right|+\left|z-5\right|\ge0\forall x,y,z\)
Dấu " = " xảy ra khi và chỉ khi \(\left\{{}\begin{matrix}\left|x+\frac{2}{3}\right|=0\\\left|y-\frac{3}{4}\right|=0\\\left|z-5\right|=0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=-\frac{2}{3}\\x=\frac{3}{4}\\z=5\end{matrix}\right.\)
Vậy GTNN = 0 khi x = -2/3,y = 3/4,z = 5
Bài cuối tự làm :)))

\(\frac{3}{4}\cdot\frac{8}{9}\cdot\frac{15}{16}\cdot...\cdot\frac{9999}{10000}\)
\(=\frac{1\cdot3}{2^2}\cdot\frac{2\cdot4}{3^2}\cdot\frac{3\cdot5}{4^2}\cdot...\cdot\frac{99\cdot101}{100^2}\)
\(=\frac{\left(1\cdot3\right)\left(2\cdot4\right)\left(3\cdot5\right)...\left(99\cdot101\right)}{2^2\cdot3^2\cdot4^2\cdot...\cdot100^2}\)
\(=\frac{\left(1\cdot2\cdot3\cdot...\cdot99\right)\left(3\cdot4\cdot5\cdot101\right)}{\left(2\cdot3\cdot4\cdot...\cdot100\right)\left(2\cdot3\cdot4\cdot...\cdot100\right)}\)
\(=2\cdot101=202\)
\(= \frac{1 \cdot 3}{2^{2}} \cdot \frac{2 \cdot 4}{3^{2}} \cdot \frac{3 \cdot 5}{4^{2}} \cdot . . . \cdot \frac{99 \cdot 101}{10 0^{2}}\)
\(= \frac{\left(\right. 1 \cdot 3 \left.\right) \left(\right. 2 \cdot 4 \left.\right) \left(\right. 3 \cdot 5 \left.\right) . . . \left(\right. 99 \cdot 101 \left.\right)}{2^{2} \cdot 3^{2} \cdot 4^{2} \cdot . . . \cdot 10 0^{2}}\)
\(= \frac{\left(\right. 1 \cdot 2 \cdot 3 \cdot . . . \cdot 99 \left.\right) \left(\right. 3 \cdot 4 \cdot 5 \cdot 101 \left.\right)}{\left(\right. 2 \cdot 3 \cdot 4 \cdot . . . \cdot 100 \left.\right) \left(\right. 2 \cdot 3 \cdot 4 \cdot . . . \cdot 100 \left.\right)}\)
\(= 2 \cdot 101 = 202\)
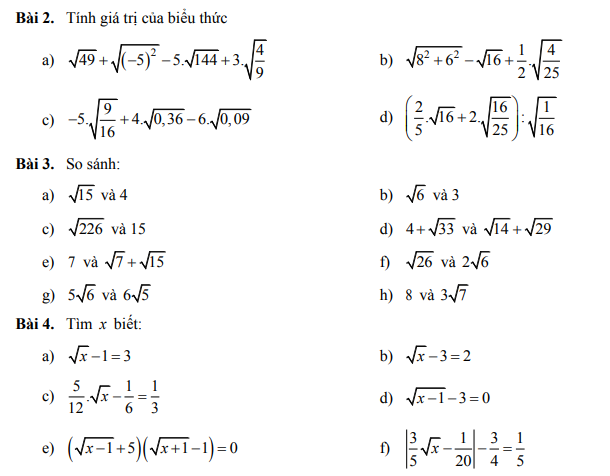 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
khoảng cách giữa các số hạng là số lẻ có 1 chữ số theo thứ tự từ bé đến lớn
\(D=\left\lbrace m\vert m=n^2\in\mathbb{N}^{\ast},n\le5\right\rbrace\)