Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: Ta có: AB=AD
nên A nằm trên đường trung trực của BD(1)
Ta có: CB=CD
nên C nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
b: Xét ΔBAC và ΔDAC có
AB=AD
AC chung
BC=DC
Do đó: ΔBAC=ΔDAC
Suy ra: \(\widehat{B}=\widehat{D}\)
=>\(\widehat{B}=\widehat{D}=\dfrac{200^0}{2}=100^0\)

Bài 1:
Do E là hình chiếu của D trên AB:
=) DE\(\perp\)AB tại E
=) \(\widehat{DE\text{A}}\)=900
Do F là hình chiếu của D trên AC:
=) DF\(\perp\)AC
=) \(\widehat{DFA}\)=900
Xét tứ giác AEDF có :
\(\widehat{D\text{E}F}\)=\(\widehat{E\text{A}F}\)=\(\widehat{DFA}\) (cùng bằng 900)
=) Tứ giác AEDF là hình chữ nhật
Xét hình chữ nhật AEDF có :
AD là tia phân giác của \(\widehat{E\text{A}F}\)
=) AEDF là hình vuông

a: Xét tứ giác ABED có
góc BAD=góc ADE=góc BED=90 độ
nên ABED là hình chữ nhật
b: Xét tứ giác BMCD có
BM//CD
BM=CD
Do đo; BMCD là hình bình hành
c:
Gọi O là trung điểm của AE
góc AIE=90 độ
mà IO là trung tuyến
nên IO=AE/2=BD/2
Xét ΔIBD có
IO là trung tuyến
IO=BD/2
Do đó: ΔIBD vuông tại I

Bài 1:
a,xét tam giác ABC và tam giác EDC có:
AB=DE(gt)
DC=DC(gt)
góc EDC=ABC=(180 độ-ADC)
=>tam giác ABC=EDC(c.g.c)
b,tam giác ABC=EDC
=.AC=EC
=>tam giác ACE cân tại C
=> góc DAC=DEC(1)
Mặt khác 2 tam giác trên bằng nhau
=>DAC=DEC(2)
Từ (1) và (2)=>DAC=BAC
=> góc AC là tia pg của A
---------------------------đợi mik nghiên cứu bài 2 đã chà nha học tốt---------------------------------
AB//CD=>A+B=180 độ (hai góc trong cùng phía)(1)
A-D=20 độ(2)
Lấy (1)+(2)=>A+D+A-D=180 độ +20=> 2A=200=>A=100 độ
A+B=180 độ=>D=180 độ=>D=180 -A=180-100=80 độ
AB//CD>B+C=180 độ (hai góc trong cùng phía)
Hay AC+C=180 độ=>3C=180 độ =>C=60 độ
B+C=180 độ=>B=180 -C=180-60=120 độ
--------------------------------------------học tốt-------------------------------

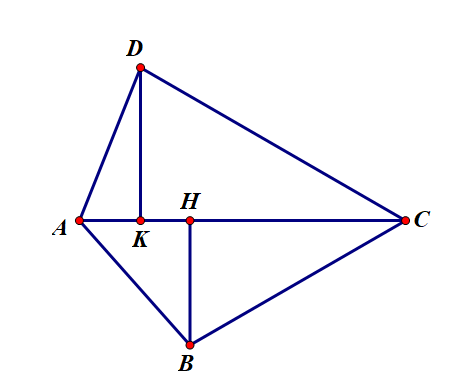
Kẻ các đường cao BH,DK xuống đường chéo ACAC là phân giác của góc C nên ACDˆ=ACBˆ=30o

pls ai bt trl nhanh đc k sp đi hok r
Phân tích:
1. Xét tam giác △ACD:
2. Xét điểm K:
3. Yêu cầu: Tính góc ∠ADK
Ta cần tính góc tạo bởi hai đoạn DA và DK.
Ta biết:
Đặt hệ trục tọa độ:
Ta chọn tọa độ sao cho đơn giản:
⇒ Khi đó, ta dễ dàng thấy ∠A = 90° (góc vuông giữa hai trục).
Tìm điểm C:
Giả sử điểm C sao cho CA = CD.
Gọi C(x, y), ta có:
Vì CA = CD ⇒ CA² = CD²:
\(x^{2} + y^{2} = \left(\right. x - a \left.\right)^{2} + y^{2} \Rightarrow x^{2} = \left(\right. x - a \left.\right)^{2}\)
Giải phương trình:
\(x^{2} = x^{2} - 2 a x + a^{2} \Rightarrow - 2 a x + a^{2} = 0 \Rightarrow x = \frac{a}{2}\)
⇒ Vậy điểm C có hoành độ \(\frac{a}{2}\), tung độ y tùy ý. Ta chọn y > 0 cho phù hợp với hình vẽ.
Tìm điểm K:
⇒ Gọi tọa độ B là (0, b), C là \(\left(\right. \frac{a}{2} , y \left.\right)\), thì K có tọa độ:
\(K = 2 \cdot C - B = 2 \left(\right. \frac{a}{2} , y \left.\right) - \left(\right. 0 , b \left.\right) = \left(\right. a , 2 y - b \left.\right)\)
Bây giờ tính góc ∠ADK
Ta có 3 điểm:
Tính góc ∠ADK là góc giữa hai vectơ:
Góc giữa hai vectơ DA và DK là góc giữa vectơ ngang và vectơ thẳng đứng.
⇒ Vì một vectơ nằm ngang, một vectơ nằm thẳng đứng ⇒ góc giữa chúng là 90°.
\(\boxed{\angle A D K = 90^{\circ}}\)